
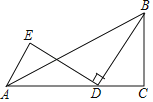
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
【答案】![]()
【解析】
由旋转的性质可知BD=DE,∠C=90°,则容易想到构造一个直角三角形与Rt△BCD全等,即过E点作EH⊥AD于点H,设CD=x,则可用x表示AE的长,从而判断什么时候AE取得最小值.
设CD=x,则AD=5﹣x,
过点E作EH⊥AD于点H,如图:
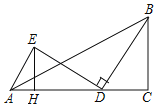
由旋转的性质可知BD=DE,
∵∠ADE+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠ADE=∠CBD,
又∵∠EHD=∠C,
∴△BCD≌△DHE,
∴EH=CD=x,DH=BC=3.
∵AD=5﹣x,
∴AH=AD﹣DH=5﹣x﹣3=2﹣x,
∵在Rt△AEH中,AE2=AH2+EH2=(2﹣x)2+x2=2x2+4x+4=2(x﹣1)2+2,
所以当x=1时,AE2取得最小值2,即AE取得最小值![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】今年,6月7日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
小丽 | 每个定价3元,每天能卖出500个.若这种粽子的售价每上涨0.1元,其销售量将减少10个 |
小华 | 照你说,若要实现每天800元的销售利润,那该如何定价?别忘了,根据物价局规定,售价不能超过进价的 |
小明 | 若按照物价局规定的最高售价,每天的利润会超过800元吗?请判断并说明理由 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且EO=2DE,则ED的长为( )

A.![]() B.2
B.2![]() C.1D.2
C.1D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
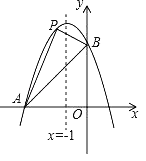
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2;
所以图中P1,P2即为所求的点.
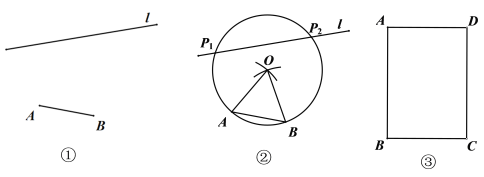
(1)在图②中,连接P1A,P1B,证明∠AP1B=30°;
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(3)已知矩形ABCD,若BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.

(1)求抛物线的解析式;
(2)如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;
(3)如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PMPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:如图,过圆外一点作圆的切线.
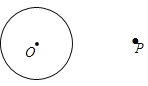
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C.
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点.
(3)作直线PA,PB.
所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
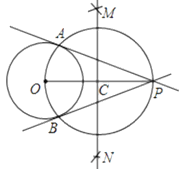
请回答:
(1)连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_________.
(2)如果⊙O的半径等于3,点P到切点的距离为4,求点A与点B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)求这个二次函数图象的顶点坐标及对称轴;
(2)指出该图象可以看作抛物线y=2x2通过怎样平移得到?
(3)在给定的坐标系内画出该函数的图象,并根据图象回答:当x取多少时,y随x增大而减小;当x取多少时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,交y 轴于点C:
,交y 轴于点C:

(1)求抛物线的顶点坐标.
(2)点![]() 为抛物线上一点,是否存在点
为抛物线上一点,是否存在点![]() 使
使![]() ,若存在请直接给出点
,若存在请直接给出点![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com