
����Ŀ���Ķ�������ϣ�
��ѧϰ��Բ����һ��ʱ����ʦ��ͬѧ�Dz�����һ���߹���ͼ�⣺
�߹���ͼ����ͼ����Բ��һ����Բ������.
��֪��PΪ��O��һ��.
������������P�ġ�O������.
С�����������£���ͼ��
(1)����OP�����߶�OP�Ĵ�ֱƽ����MN��OP�ڵ�C.
(2)�Ե�CΪԲ�ģ�CO�ij�Ϊ�뾶��Բ������O��A��B����.
(3)��ֱ��PA��PB.
����ֱ��PA��PB����������������.
��ʦ��ΪС����������ȷ.
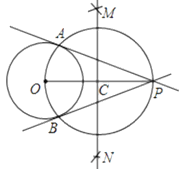
��ش�
(1)����OA��OB��֤��OAP����OBP��90������������_________.
(2)�����O�İ뾶����3����P���е�ľ���Ϊ4�����A���B֮��ľ���.
���𰸡���1��ֱ�����Ե�Բ�ܽ���ֱ�ǣ���2��![]()
��������
��1��ֱ�Ӹ���Բ�ܽǶ������ɵó���OAP=��OBP=90�㣬�����ߵ����ʼ��ɵó����ۣ�
��2������OA,AB��OP�ڵ�E,�������ߵ����ʣ��ɵá�OAP =90�㣬AE��OP,���ݹ��ɶ������OP,�ٸ��ݵ���������AE,�������AB.
��1���⣺����OA��OB��֤��OAP=��OBP=90�㣬�������ǣ�ֱ�����Ե�Բ�ܽ���ֱ�ǣ�
�ɴ˿�֤��ֱ��PA��PB���ǡ�O�����ߣ��������ǣ������뾶��ˣ�����뾶��ֱ��ֱ����Բ�����ߣ�
�ʴ�Ϊ��ֱ�����Ե�Բ�ܽ���ֱ�ǣ������뾶��ˣ�����뾶��ֱ��ֱ����Բ�����ߣ�
��2������OA,AB��OP�ڵ�E,
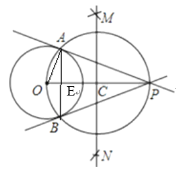
��ΪPA�ǡ�O�����ߣ�
������OAP =90�㣬
��ֱ��������OAP�У��ɹ��ɶ����ɵ�:OP=5,
��ΪAE��OP,
����![]() ,
,
����AE=![]() ,
,
����AB=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
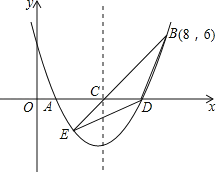
����Ŀ����ͼ�����κ���y��![]() x2+bx+c��ͼ��x����A��D���㲢����B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6����
x2+bx+c��ͼ��x����A��D���㲢����B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6����
��1������κ����Ľ���ʽ��
��2���ö��κ����ĶԳ��ύx����C�㣬����BC�����ӳ�BC����������E�㣬����BD��DE������BDE�������
��3������������һ������P����A��D���㹹����ADP���Ƿ����2S��ADP��S��BCD�������������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�����������е�ÿ��С�����εı߳�����1,ÿ��С�����εĶ���������.��ABC����������A,B,C���ڸ����,����ABC�Ƶ�A��ʱ�뷽����ת90���õ���AB��C��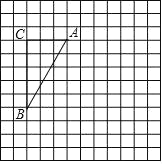
(1)��������������,������AB��C����
(2)�ֱ���ת�����У���B��C������·����
(3)�����߶�BC�ڱ任��B��C���Ĺ�����ɨ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90����BC��3��AC��5����DΪ�߶�AC��һ���㣬���߶�BD�Ƶ�D��ʱ����ת90������B�Ķ�Ӧ��ΪE������AE����AE������СֵΪ_____��
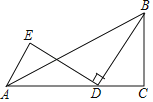
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˼�μ����е���̨��֯����ĵ���������������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ�����������˼�����ᣬ������˼��������������������ʹ�ã�ʹ����������һ�ο�����������ȥ������һ���һ������ѡ�.
��1�������˼���������������ڵ�һ����ѡ����ʹ�ã�����ͨ�صĸ��ʣ�
��2�������˼ÿ����ѡ���ʹ��һ��������"�������б�������״ͼ�ķ�������˳��ͨ�صĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ڣ���������ͬһֱ���ϵĵ�A��B��C����ͼ��ʾ.��O����A��B��C�ľ��������a(aΪ����)������O�ľ������a�����е����ͼ��G����ABC��ƽ���߽�ͼ��G�ڵ�D������AD��CD.
(1)��֤��AD=CD.
(2)����D��DE��BA������ΪE����DF��BC������ΪF���ӳ�DF��ͼ��G�ڵ�M������CM.��AD=CM���ж�ֱ��DE��ͼ��G��λ�ù�ϵ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��D��Բ�ϣ�![]() ��
��![]() ������C��CE��AD�ӳ����ڵ�E��
������C��CE��AD�ӳ����ڵ�E��
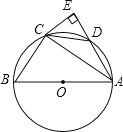
��1����֤��CE�ǡ�O�����ߣ�
��2����BC��3��AC��4����CE��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() �����κ���
�����κ���![]() ��ͼ����
��ͼ����![]() �͵�
�͵�![]() ������Ϊ
������Ϊ![]() ���Գ�����һ�κ�����ͼ���ཻ�ڵ�
���Գ�����һ�κ�����ͼ���ཻ�ڵ�![]() ��
��
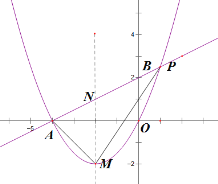
��1����һ�κ����Ľ���ʽ�Լ�![]() �㣬
�㣬![]() ������ꣻ
������ꣻ
��2����![]() �����ꣻ
�����ꣻ
��3����![]() ������һ��
������һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ���ơ�
���ơ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��18��BC��12��������DEFG�Ķ���E��F����ABC�ڣ�����D��G�ֱ���AB��AC�ϣ�AD��AG��DG��6�����F��BC�ľ���Ϊ( )
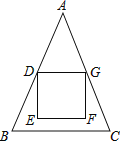
A.1B.2C.12![]() ��6D.6
��6D.6![]() ��6
��6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com