
【题目】如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下:
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于P1,P2;
所以图中P1,P2即为所求的点.
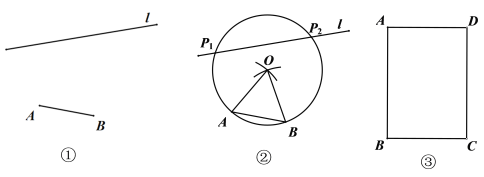
(1)在图②中,连接P1A,P1B,证明∠AP1B=30°;
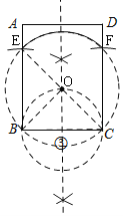
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(3)已知矩形ABCD,若BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为______________.
【答案】(1)30°;(2)详见解析;(3)2≤m<![]()
【解析】
(1)由等边三角形得:∠AOB=60°,则根据圆周角定理可得:∠AP1B=30°;
(2)作等腰直角三角形BEC,BFC,再作△EBC的外接圆,可得圆心角∠BOC=90°,则BC所对的圆周角都是45°;
(3)先确定⊙O,根据同弧所对的圆周角相等,可得AD在四边形GEFH内部时符合条件,再进行求解即可;
答案:(1)∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
由图②得:∠AP1B= ∠AOB=30°;
(2)如图③,①以B、C为圆心,以BC为半径作圆,交AB、DC于E、F,
②作BC的中垂线,连接EC,交于O,
③以O为圆心,OE为半径作圆,
则 上所有的点(不包括E、F两点)即为所求;
(3)如图:作⊙O
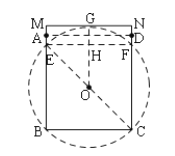
∵BE=BC=2
∴CE=![]()
∴⊙O的半径为![]() v2,即OE=0G=
v2,即OE=0G=![]() ,
,
∵OG⊥EF
∴EH=1,
∴Oн=1,
∴GH=![]() -1,
-1,
∴BE≤AB<MB,
∴2≤m<2+![]() -1,即2<m<
-1,即2<m<![]() +1,
+1,
故答案为:2≤m<![]()


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A逆时针方向旋转90°得到△AB′C′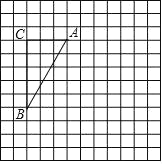
(1)在正方形网格中,画出△AB′C′;
(2)分别画出旋转过程中,点B点C经过的路径;
(3)计算线段BC在变换到B′C′的过程中扫过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
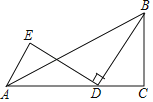
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇思参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题奇思都不会,不过奇思还有两个“求助”可以使用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果奇思两次“求助”都在第一道单选题中使用,求他通关的概率;
(2)如果奇思每道单选题各使用一次“求助",请用列表法或画树状图的方法求他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在圆上,![]() =
=![]() ,过点C作CE⊥AD延长线于点E.
,过点C作CE⊥AD延长线于点E.
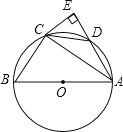
(1)求证:CE是⊙O的切线;
(2)若BC=3,AC=4,求CE和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
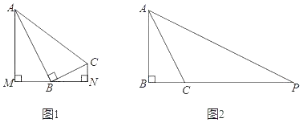
【题目】在∠ABC中,∠ABC=90°,tan∠BAC=![]() .
.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com