
【题目】如图,在矩形ABCD中对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且EO=2DE,则ED的长为( )

A.![]() B.2
B.2![]() C.1D.2
C.1D.2
科目:初中数学 来源: 题型:
【题目】阅读理解题:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,我们来进行以下的探索:
)2,我们来进行以下的探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b
,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b![]() 的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= .
)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)若a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
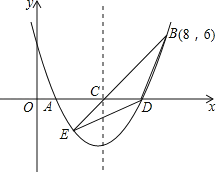
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式;
(2)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积;
(3)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在2S△ADP=S△BCD?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
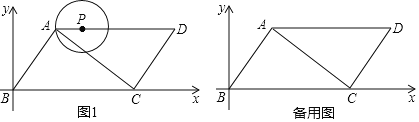
【题目】如图1,平行四边形ABCD中,以B为坐标原点建立如图所示直角坐标系,AB⊥AC,AB=3,AD=5,点P在边AD上运动(点P不与A重合,但可以与D点重合),以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1) 直接写出点A的坐标(____,____)设AP为x,直接写出P点坐标(_______,______)(用含x的代数式表示)
(2)当⊙P与边CD相切于点F时,求P点的坐标;
(3)随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,直接写出公共点的个数与相对应的AP的取值之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A逆时针方向旋转90°得到△AB′C′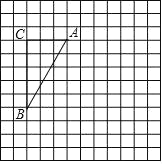
(1)在正方形网格中,画出△AB′C′;
(2)分别画出旋转过程中,点B点C经过的路径;
(3)计算线段BC在变换到B′C′的过程中扫过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
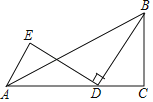
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,二次函数
,二次函数![]() 的图像经过点
的图像经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() ,对称轴与一次函数的图像相交于点
,对称轴与一次函数的图像相交于点![]() 。
。
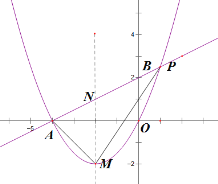
(1)求一次函数的解析式以及![]() 点,
点,![]() 点的坐标;
点的坐标;
(2)求顶点![]() 的坐标;
的坐标;
(3)在![]() 轴上求一点
轴上求一点![]() ,使得
,使得![]() 和
和![]() 相似。
相似。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com