
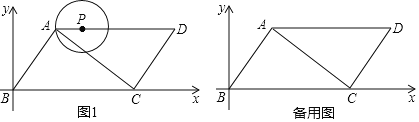
【题目】如图1,平行四边形ABCD中,以B为坐标原点建立如图所示直角坐标系,AB⊥AC,AB=3,AD=5,点P在边AD上运动(点P不与A重合,但可以与D点重合),以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1) 直接写出点A的坐标(____,____)设AP为x,直接写出P点坐标(_______,______)(用含x的代数式表示)
(2)当⊙P与边CD相切于点F时,求P点的坐标;
(3)随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,直接写出公共点的个数与相对应的AP的取值之间的关系.
【答案】(1)(1)A(![]() ,
,![]() ) P(
) P(![]() +x ,
+x , ![]() )(2)点P坐标为(
)(2)点P坐标为(![]() )(3)见解析.
)(3)见解析.
【解析】
(1)过A作x轴垂线交点为G,∴![]() 可求得:
可求得:![]() ;
;
(2)连接PF,可证得△DPF∽△DAC,利用相似三角形对应边成比例可求得:AP=PF=![]() ,从而求得P点的坐标;
,从而求得P点的坐标;
(3)以![]() 、
、![]() 、
、![]() 、5为分段点,分类讨论.
、5为分段点,分类讨论.
(1)A(![]() ,
,![]() ) P(
) P(![]() +x ,
+x , ![]() ) ;
) ;
(2)如图,连接PF

∵⊙P与边CD相切于点F
∴PF⊥CD
∵四边形ABCD是平行四边形
∴AB∥CD,且AB⊥AC
∴AC⊥CD
∴PF∥AC
∴△DPF∽△DAC
∴![]()
∴![]()
∴AP=![]()
∴点P坐标为(![]() )
)
(3)当0<AP<![]() 或
或![]() <AP≤5时,⊙P与平行四边形ABCD的边有2个公共点;
<AP≤5时,⊙P与平行四边形ABCD的边有2个公共点;
当AP=![]() 时,⊙P与平行四边形ABCD的边有3个公共点;
时,⊙P与平行四边形ABCD的边有3个公共点;
当![]() <AP<
<AP<![]() 时,⊙P与平行四边形ABCD的边有4个公共点;
时,⊙P与平行四边形ABCD的边有4个公共点;
当AP=![]() 时,⊙P与平行四边形ABCD的边有5个公共点;
时,⊙P与平行四边形ABCD的边有5个公共点;
当![]() 时,⊙P与平行四边形ABCD的边有6个公共点.
时,⊙P与平行四边形ABCD的边有6个公共点.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,6月7日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
小丽 | 每个定价3元,每天能卖出500个.若这种粽子的售价每上涨0.1元,其销售量将减少10个 |
小华 | 照你说,若要实现每天800元的销售利润,那该如何定价?别忘了,根据物价局规定,售价不能超过进价的 |
小明 | 若按照物价局规定的最高售价,每天的利润会超过800元吗?请判断并说明理由 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(![]() +3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了适合不同人群的口味,某商店对苹果味、草莓味、牛奶味的糖果混合组装成甲、乙两种袋装进行销售.甲种每袋装有苹果味、草莓味、牛奶味的糖果各10颗,乙种每袋装有苹果味糖果20颗,草莓味和牛奶味糖果各5颗.甲、乙两种袋装糖果每袋成本价分别是袋中各类糖果成本之和.已知每颗苹果味的糖果成本价为0.4元,甲种袋装糖果的售价为23.4元,利润率为30%,乙种袋装糖果每袋的利润率为20%.若这两种袋装的销售利润率达到24%,则该公司销售甲、乙两种袋装糖果的数量之比是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且EO=2DE,则ED的长为( )

A.![]() B.2
B.2![]() C.1D.2
C.1D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
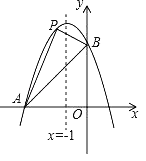
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)求这个二次函数图象的顶点坐标及对称轴;
(2)指出该图象可以看作抛物线y=2x2通过怎样平移得到?
(3)在给定的坐标系内画出该函数的图象,并根据图象回答:当x取多少时,y随x增大而减小;当x取多少时,y<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com