
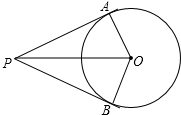
 如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于
如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
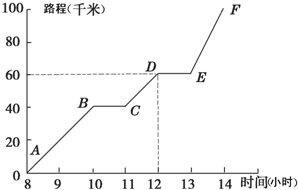 如图,描述了小明早晨8时到下午14时,骑摩托车从甲地到乙地所走路程与时间的关系,根据折线图提供的信息思考下列问题:?
如图,描述了小明早晨8时到下午14时,骑摩托车从甲地到乙地所走路程与时间的关系,根据折线图提供的信息思考下列问题:?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com