
【题目】如图,点O是边长为4的等边三角形ABC的中心,∠EOF的两边与△ABC的边AB,BC分别交于E、F,∠EOF=120°.
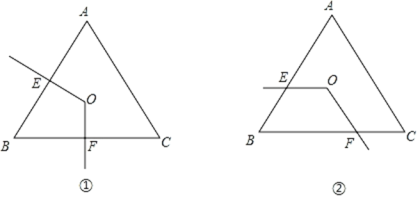
(1)如图①,当E为AB中点时,求∠EOF与△ABC的边所围成的四边形OEBF的面积;
(2)如图②,∠EOF绕点O旋转.在旋转过程中四边形OEBF的面积会改变吗?请说明理由.
【答案】(1)四边形OEBF的面积=![]() ;(2)不变,理由见解析.
;(2)不变,理由见解析.
【解析】
(1)连接OB,由等边三角形的性质可得∠ABO=∠CBO=30°,分别求出OE,OF的长,由面积公式可求解;
(2)连接OB、OC,过点O作ON⊥BC,垂足为N,由“ASA”可证△EOB≌△FOC,可得S△EOB=S△FOC,由面积公式可求解.
解:(1)连接OB,

∵点O是边长为4的等边三角形ABC的中心,
∴∠ABO=∠CBO=30°,
∵当E为AB中点时,
∴AE=BE=2,OE⊥AB,
∴∠BOE=60°,![]() ,
,
∵∠EOF=120°,
∴∠BOF=60°,
∴∠BFO=180°﹣30°﹣60°=90°,
∴BF=CF=2,
∴![]() ,
,
∴四边形OEBF的面积=![]() ;
;
(2)不变,
理由如下:连接OB、OC,过点O作ON⊥BC,垂足为N,
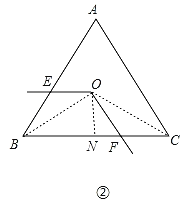
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵点O为△ABC的中心
∴∠OBC=∠OBA=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB.
∠ACB.
∴∠OBA=∠OBC=∠OCB=30°.
∴OB=OC.∠BOC=120°,
∵ON⊥BC,BC=4,
∴BN=NC=2,
∴ON=tan∠OBCBN=![]() ,
,
∴S△OBC=![]() BCON=
BCON=![]() ,
,
∵∠EOF=∠BOC=120°,
∴∠EOF﹣∠BOF=∠BOC﹣∠BOF,即∠EOB=∠FOC,
在△EOB和△FOC中,
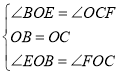
∴△EOB≌△FOC(ASA),
∴S△EOB=S△FOC,
∴![]() =
=![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
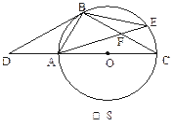
(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=![]() ,求△ACF的面积.
,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示.
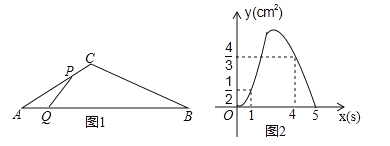
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
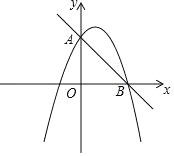
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发兼零售的文具店规定:凡一次购买铅笔300支以上(不包括300支),可以按批发价付款;购买300支以下(包括300支)只能按零售价付款,小明来该店购买铅笔,如果给学校九年级学生每人购买1支,那么只能按零售价付款,需用150元;如果多购买60支,那么可以按批发价付款,同样需用150元.
(1)这个学校九年级的学生总数在什么范围内?
(2)如果按批发价购买360支与按零售价购买300支所付款相同,那么这个学校九年级学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有![]() 个选项,第二道题有
个选项,第二道题有![]() 个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
(1)如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;
(2)从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com