
【题目】如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
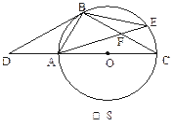
(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=![]() ,求△ACF的面积.
,求△ACF的面积.
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
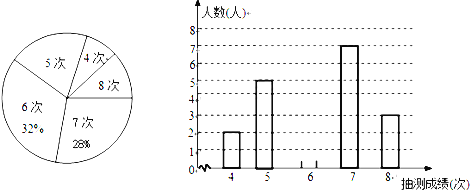
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点A(m-2,n), B(m+4,n),C(m,
过点A(m-2,n), B(m+4,n),C(m,![]() ).
).
(1)b=__________(用含m的代数式表示);
(2)求△ABC的面积;
(3)当![]() 时,均有
时,均有![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把矩形沿EF折叠后,使点D恰好落 在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
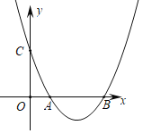
(1)求二次函数的解析式;
(2)若点![]() 为抛物线上的一点,点
为抛物线上的一点,点![]() 为对称轴上的一点,且以点
为对称轴上的一点,且以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,求点
为顶点的四边形为平行四边形,求点![]() 的坐标;
的坐标;
(3)点![]() 是二次函数第四象限图象上一点,过点
是二次函数第四象限图象上一点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,求四边形
,求四边形![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是边长为4的等边三角形ABC的中心,∠EOF的两边与△ABC的边AB,BC分别交于E、F,∠EOF=120°.
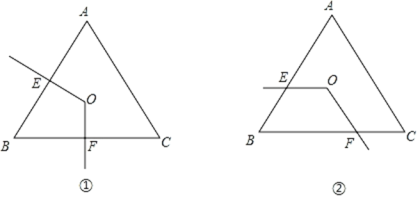
(1)如图①,当E为AB中点时,求∠EOF与△ABC的边所围成的四边形OEBF的面积;
(2)如图②,∠EOF绕点O旋转.在旋转过程中四边形OEBF的面积会改变吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,其对称轴与抛物线相交于点
,其对称轴与抛物线相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
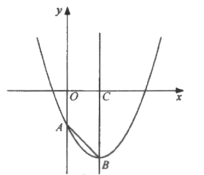
(1)求![]() 的长;
的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为![]() .若新抛物线经过原点
.若新抛物线经过原点![]() ,且
,且![]() ,求新抛物线对应的函数表达式.
,求新抛物线对应的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com