
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
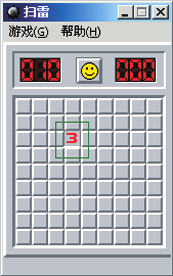
【题目】如图是计算机中“扫雷”游戏的画面.在一个有 9×9 个方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现了如图所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域有3颗地雷.为了最大限 度的避开地雷,下一步应该点击的区域是___. (填“A”或“B”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量![]() 件与销售单价
件与销售单价![]() 元之间的关系式;
元之间的关系式;
(2)当销售单价![]() 定为多少,才能使每天所获销售利润最大?最大利润是多少?
定为多少,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
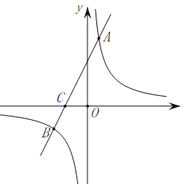
【题目】在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 有最大值,如果存在,请求出点
有最大值,如果存在,请求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
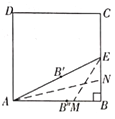
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
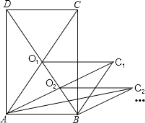
【题目】如图,矩形![]() 的面积为
的面积为![]() ,它的两条对角线交于点
,它的两条对角线交于点![]() ,以
,以![]() 、
、![]() 为两邻边作平行四边形
为两邻边作平行四边形![]() ,平行四边形
,平行四边形![]() 的对角线交于点
的对角线交于点![]() ,同样以
,同样以![]() 、
、![]() 为两邻边作平行四边形
为两邻边作平行四边形![]() ,…,依此类推,则平行四边形
,…,依此类推,则平行四边形![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
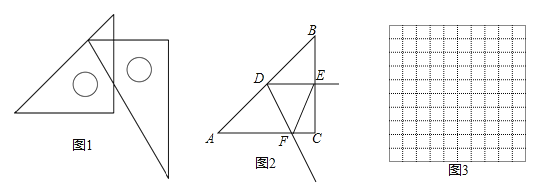
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com