
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
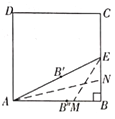
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (k ≠ 0) 在第一象限内的图象交于点A(1,m).
(k ≠ 0) 在第一象限内的图象交于点A(1,m).
(1) 求反比例函数的表达式;
(2) 点B在反比例函数的图象上, 且点B的横坐标为2. 若在x轴上存在一点M,使MA+MB的值最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线 ![]() 经过
经过 ![]() ,
, ![]() 两点,与
两点,与 ![]() 轴相交于点
轴相交于点 ![]() ,连接
,连接 ![]() .点
.点 ![]() 为抛物线上一动点,过点
为抛物线上一动点,过点 ![]() 作
作 ![]() 轴的垂线
轴的垂线 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() .
.
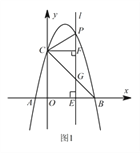
Ⅰ 求抛物线的表达式;
Ⅱ 当 ![]() 位于
位于 ![]() 轴右边的抛物线上运动时,过点
轴右边的抛物线上运动时,过点 ![]() 作
作 ![]() 直线
直线 ![]() ,
, ![]() 为垂足.当点
为垂足.当点 ![]() 运动到何处时,以
运动到何处时,以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似?并求出此时点
相似?并求出此时点 ![]() 的坐标;
的坐标;
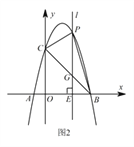
Ⅲ 如图2,当点 ![]() 在位于直线
在位于直线 ![]() 上方的抛物线上运动时,连接
上方的抛物线上运动时,连接 ![]() ,
, ![]() .请问
.请问 ![]() 的面积
的面积 ![]() 能否取得最大值?若能,请求出最大面积
能否取得最大值?若能,请求出最大面积 ![]() ,并求出此时点
,并求出此时点 ![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
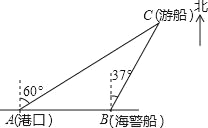
A. ![]() B.
B. ![]() C. sin37°D. cos37°
C. sin37°D. cos37°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥,从2009年开工建造,于2018年10月24日正式通车.其全长55公里,连接港珠澳三地,集桥、岛、隧于一体,是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.73,tan20°≈0.36,结果精确到0.1)
≈1.73,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
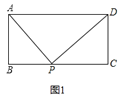
【题目】已知矩形![]() 和点
和点![]() ,当点
,当点![]() 在
在![]() 上任一位置(如图
上任一位置(如图![]() 所示)时,易证得结论:
所示)时,易证得结论:![]() ,请你探究:当点
,请你探究:当点![]() 分别在图
分别在图![]() 、图
、图![]() 中的位置时,
中的位置时,![]() 、
、![]() 、
、![]() 和
和![]() 又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图
又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图![]() 证明你的结论.
证明你的结论.
答:对图![]() 的探究结论为________;
的探究结论为________;
对图![]() 的探究结论为________;
的探究结论为________;


查看答案和解析>>
科目:初中数学 来源: 题型:
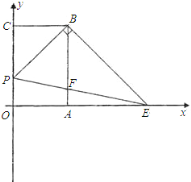
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.在运动的过程中,写出以P、O、E为顶点的三角形与△ABE相似时t的值为_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com