练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

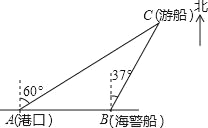
    【题目】一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以每小时40海里的速度前往救援，则海警船到达事故船C处所需的时间大约为（单位：小时）（　　）

    A. B. C. sin37°D. cos37°

    【答案】B

    【解析】

    过点C作CD⊥AB交AB延长线于D．先解Rt△ACD得出CDAC=40海里，再解Rt△CBD中，得出BC海里，然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间．

    如图，过点C作CD⊥AB交AB延长线于D．

    在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80，∴CDAC=40．

    在Rt△CBD中，∵∠CDB=90°，∠BCD=37°，∴BC，∴海警船到大事故船C处所需的时间大约为：40（小时）．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

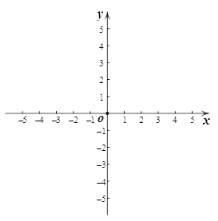
    【题目】在平面直角坐标系xOy中，⊙C的半径为r，给出如下定义：若点P的横、纵坐标均为整数，且到圆心C的距离d≤r，则称P为⊙C 的关联整点.

    （1）当⊙O的半径r=2时，在点D（2，-2），E（-1，0），F（0，2）中，为⊙O的关联整点的是 ；

    （2）若直线上存在⊙O的关联整点，且不超过7个，求r的取值范围；

    （3）⊙C的圆心在x轴上，半径为2，若直线上存在⊙C的关联整点，求圆心C的横坐标t的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

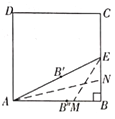
    【题目】如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF．，GH．

    （1）填空：∠AHC　 　∠ACG；（填“＞”或“＜”或“＝”）

    （2）线段AC，AG，AH什么关系？请说明理由；

    （3）设AE＝m，

    ①△AGH的面积S有变化吗？如果变化．请求出S与m的函数关系式；如果不变化，请求出定值．

    ②请直接写出使△CGH是等腰三角形的m值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年8月．山西龙城将迎来全国第二届青年运动会，盛会将至，整个城市已经进入了全力准备的状态．太职学院足球场作为一个重要比赛场馆．占地面积约24300平方米．总建筑面积4790平方米，设有2476个座位，整体建筑简洁大方，独具特色．2018年3月15日该场馆如期开工，某施工队负责安装该场馆所有座位，在安装完476个座位后，采用新技术，效率比原来提升了．结来比原计划提前4天完成安装任务．求原计划每天安装多少个座位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成相应任务．

    古希腊数学家，天文学家欧多克索斯（Eudoxus，约前400—前347）曾提出：能否将一

    条线段分成不相等的两部分．使较短线段与较长线段的比等于较长线段与原线段的比，这个相等的比就是，黄金分割在我们生活中有广泛运用．黄金分割点也可以用折纸的方式得到．

    第一步：裁一张正方形的纸片，先折出的中点，然后展平，再折出线段，再展平；

    第二步：将纸片沿折叠，使落到线段上，的对应点为，展平；

    第三步：沿折叠，使落在上，的对应点为，展平，这时就是的黄金分割点．

    古希腊数学家，天文学家欧多克索斯（Eudoxus，约前400—前347）曾提出：能否将一

    条线段分成不相等的两部分．使较短线段与较长线段的比等于较长线段与原线段的比，这个相等的比就是，黄金分割在我们生活中有广泛运用．黄金分割点也可以用折纸的方式得到．

    第一步：裁一张正方形的纸片，先折出的中点，然后展平，再折出线段，再展平；

    第二步：将纸片沿折叠，使落到线段上，的对应点为，展平；

    第三步：沿折叠，使落在上，的对应点为，展平，这时就是的黄金分割点．

    任务：（1）试根据以上操作步骤证明就是的黄金分割点；

    （2）请写出一个生活中应用黄金分割的实际例子．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

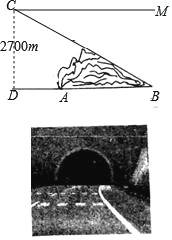
    【题目】乌鞘岭隧道群是连霍国道主干线上隧道最密集、路线最长、海拔最高、地质条件最复杂、施工难度最大的咽喉工程．乌鞘岭特长公路隧道群的全部贯通，将使连霍国道主干线在甘肃境内1608公里路段全部实现高速化，同时也使甘肃河西五市与省会兰州及东南沿海省、市实现全线高速连接．如图，在建设中为确定某隧道AB的长度，测量人员在离地面2700米高度C处的飞机上，测得正前方A、B两点处的俯角分别是60°和30°，求隧道AB的长（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

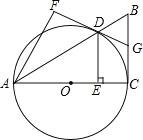
    【题目】已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．

    （1）如图1，求证：KE=GE；

    （2）如图2，连接CABG，若∠FGB=∠ACH，求证：CA∥FE；

    （3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=，AK=，求CN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，直线l：y=x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y=x2+bx+c经过点B，与直线l的另一个交点为C（4，n）．

    （1）求n的值和抛物线的解析式；

    （2）点D在抛物线上，DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2），设点D的横坐标为t（0＜t＜4），矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

    （3）将△AOB绕平面内某点M旋转90°或180°，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，那么我们就称这样的点为“落点”，请直接写出“落点”的个数和旋转180°时点A1的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知Rt△ABC中，∠ACB=90°，以AC为直径的圆O交斜边AB于D．过D作DE⊥AC于E，将△ADE沿直线AB翻折得到△ADF．

    （1）求证：DF是⊙O的切线；

    （2）若⊙O的半径为10，sin∠FAD=，延长FD交BC于G，求BG的长．

    查看答案和解析>>

    同步练习册答案