
【题目】如图,己知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,其对称轴与抛物线相交于点
,其对称轴与抛物线相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
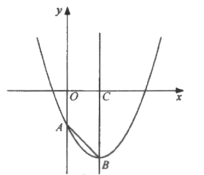
(1)求![]() 的长;
的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为![]() .若新抛物线经过原点
.若新抛物线经过原点![]() ,且
,且![]() ,求新抛物线对应的函数表达式.
,求新抛物线对应的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先利用函数关系式求出点A、B的坐标,再利用两点间的距离公式即可求得AB的长;
(2)根据A、B两点坐标结合三角函数可求得∠POA=∠ABC=45°,进而可判断点P在在一、三象限或二、四象限的角平分线上,分情况讨论,设点P坐标为(a,a)或(-a,a),利用顶点式表示出新抛物线的函数表达式,再将原点O的坐标代入计算即可.
解:(1)当x=0时,y=-1,
∴点A坐标为(0,-1),
∵![]()
∴![]()
∴点B坐标为(1,-2),
∴![]() ;
;
(2)∵点A坐标为(0,-1),点B坐标为(1,-2),
∴tan∠ABC=![]() ,
,
∴∠ABC=45°,
∵∠POA=∠ABC,
∴∠POA=45°,
∴点P在一、三象限或二、四象限的角平分线上,
当点P在一、三象限的角平分线上时,
设点P坐标为(a,a)
则设此时新抛物线的解析式为![]()
∵新抛物线经过原点![]() ,
,
∴将(0,0)代入,得![]()
解得![]() (舍去)
(舍去)
∴![]() ,
,
即![]() ,
,
当点P在二、四象限的角平分线上时,
设点P坐标为(-a,a)
则设此时新抛物线的解析式为![]()
∵新抛物线经过原点![]() ,
,
∴将(0,0)代入,得![]()
解得![]() (舍去)
(舍去)
∴![]() ,
,
即![]() ,
,
综上所述,新抛物线对应的函数表达式为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图8,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
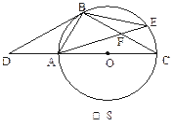
(1)求证:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=![]() ,求△ACF的面积.
,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
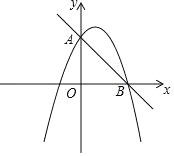
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发兼零售的文具店规定:凡一次购买铅笔300支以上(不包括300支),可以按批发价付款;购买300支以下(包括300支)只能按零售价付款,小明来该店购买铅笔,如果给学校九年级学生每人购买1支,那么只能按零售价付款,需用150元;如果多购买60支,那么可以按批发价付款,同样需用150元.
(1)这个学校九年级的学生总数在什么范围内?
(2)如果按批发价购买360支与按零售价购买300支所付款相同,那么这个学校九年级学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片ABC中,∠C=90°,AC=3cm,BC=4m,点D,E分别在边AC,AB上,点F是边BC的中点.现将该纸片沿DE折叠,使点A与点F重合,则AE=_____cm.
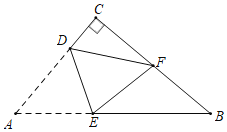
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
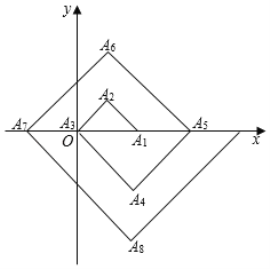
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有![]() 个选项,第二道题有
个选项,第二道题有![]() 个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
(1)如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;
(2)从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
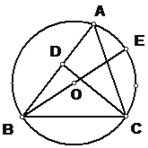
【题目】已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)已知CD=6、AD=3、BD=8,求⊙O的直径BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com