
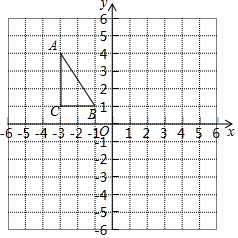
 如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.
如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.分析 (1)根据平面直角坐标系写出各点的坐标即可;
(2)横坐标乘以-1变为原来的相反数,再根据网格结构找出对应点的位置,然后顺次连接即可;
(3)根据全等三角形对应边相等,分∠CAP=∠ACB=90°和∠ACP=∠ACB=90°两种情况讨论求解.
解答  解:(1)A(-3,4)、B(-1,1)、C(-3,1);
解:(1)A(-3,4)、B(-1,1)、C(-3,1);
(2)如图所示,两个三角形关于y轴对称;
故答案为:y轴;
(3)若∠CAP=∠ACB=90°,则点P的坐标为(-1,4)或(-5,4),
若∠ACP=∠ACB=90°,则点P的坐标为(-5,1),
综上所述,点P的坐标为(-1,4)、(-5,4)或(-5,1).
点评 本题考查了利用轴对称设计图案,全等三角形的判定,熟练掌握网格结构,准确找出对应点的位置是解题的关键.


科目:初中数学 来源: 题型:填空题
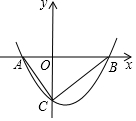 平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.
平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
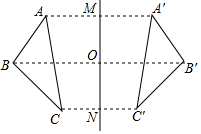 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
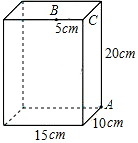 一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )| A. | 10$\sqrt{5}$cm | B. | 25cm | C. | 5$\sqrt{29}$cm | D. | 5$\sqrt{37}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “该运动员两次的射击成绩都是9环”属于随机事件 | |
| B. | “该运动员一次的射击成绩为10环,一次的射击成绩为0环”属于不可能事件 | |
| C. | “该运动员两次的射击成绩的总成绩为21环”属于必然事件 | |
| D. | 该运动员一次的射击成绩大于6环的可能性比大于8环的可能性小 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).
如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com