
分析 (1)将点(-1,0)代入可得a的值,再将解析式配方成顶点式即可得出答案;
(2)将a=a1,x=m代入y=ax2+x+2中,可求a1,同理可求a2,利用作差法求a1-a2,并化简,根据点A,B在x轴的正半轴上,且点A在点B的左边,得0<m<n,由此判断a1-a2的符号,判断a1与a2的大小.
解答 解:(1)将点(-1,0)代入得:a-1+2=0,
解得:a=-1,
∴y=-x2+x+2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴顶点坐标为($\frac{1}{2}$,$\frac{9}{4}$);
(2)方法一:∵当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点A(m,0),
∴0=a1m2+m+2①,
∵当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点B(n,0),
∴0=a2n2+n+2②,
∴a1=$\frac{-m-2}{{m}^{2}}$,a2=$\frac{-n-2}{{n}^{2}}$,
∴a1-a2=$\frac{-m-2}{{m}^{2}}$-$\frac{-n-2}{{n}^{2}}$=$\frac{-m{n}^{2}-2{n}^{2}+n{m}^{2}+2{m}^{2}}{{m}^{2}{n}^{2}}$=$\frac{mn(m-n)+2(m+n)(m-n)}{{m}^{2}{n}^{2}}$=$\frac{(mn+2m+2n)(m-n)}{{m}^{2}{n}^{2}}$,
∵点B在点A的左边,且A、B均在x轴正半轴,
∴m>0,n>0,m<n,
∴mn+2m+2n>0,m-n<0,m2n2>0,
∴a1-a2=$\frac{(mn+2m+2n)(m-n)}{{m}^{2}{n}^{2}}$<0,
∴a1<a2.
方法二:
抛物线y=ax2+x+2的对称轴为x=-$\frac{1}{2a}$,
当a>0时,x=-$\frac{1}{2a}$<0,
此时,抛物线y=ax2+x+2的对称轴在y轴的左侧,
又∵抛物线y=ax2+x+2与y轴相交于点(0,2),
∴抛物线y=ax2+x+2与x轴的正半轴无交点.
∴a>0不合题意;
当a<0时,即a1<0,a2<0.
经过点A的抛物线y=a1x2+x+2的对称轴为x=-$\frac{1}{2{a}_{1}}$,
经过点B的抛物线y=a2x2+x+2的对称轴为x=-$\frac{1}{2{a}_{2}}$,
∵点A在点B的左边,且抛物线经过点(0,2),
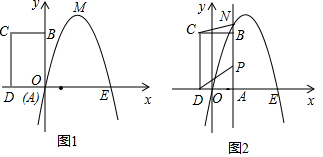
(此时两条抛物线如图所示).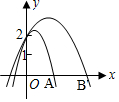
∴直线x=-$\frac{1}{2{a}_{1}}$在直线x=-$\frac{1}{2{a}_{2}}$的左侧,
∴-$\frac{1}{2{a}_{1}}$<-$\frac{1}{2{a}_{2}}$,
∴a1<a2.
点评 本题考查了二次函数的综合运用.关键是由已知条件求抛物线解析式,根据抛物线解析式求函数最大值,确定函数的正整数值,再根据函数的正整数值求对应的x值,根据函数式求a1,a2的表达式,利用作差法比较a1,a2的大小.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:选择题
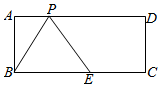 如图,在长方形ABCD中,AB=4,BC=9,点E在BC上,且BE=5,P是长方形ABCD边上的一个动点,在点P运动的过程中,使△PBE为等腰三角形的点P位置共有( )
如图,在长方形ABCD中,AB=4,BC=9,点E在BC上,且BE=5,P是长方形ABCD边上的一个动点,在点P运动的过程中,使△PBE为等腰三角形的点P位置共有( )| A. | 6处 | B. | 5处 | C. | 4处 | D. | 3处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
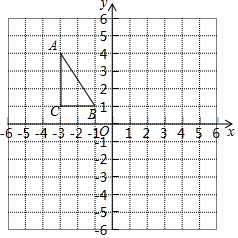 如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.
如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
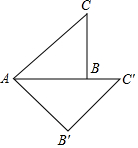 如图,已知△ABC是等腰直角三角形,以点A为中心,将△ABC顺时针旋转45°,得到△AB′C′,则∠CAB′的度数为( )
如图,已知△ABC是等腰直角三角形,以点A为中心,将△ABC顺时针旋转45°,得到△AB′C′,则∠CAB′的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com