
ЁОЬтФПЁПдкжБНЧЬнаЮOABCжаЃЌCBЁЮOAЃЌЁЯCOAЃН90ЁуЃЌCBЃН3ЃЌOAЃН6ЃЌBAЃН3![]() ЃЎЗжБ№вдOAЁЂOCБпЫљдкжБЯпЮЊxжсЁЂyжсНЈСЂШчЭМ1ЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ
ЃЎЗжБ№вдOAЁЂOCБпЫљдкжБЯпЮЊxжсЁЂyжсНЈСЂШчЭМ1ЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊDЁЂEЗжБ№ЮЊЯпЖЮOCЁЂOBЩЯЕФЕуЃЌODЃН5ЃЌOEЃН2EBЃЌжБЯпDEНЛxжсгкЕуFЃЌЙ§ЕуEзїEGЁЭxжсгкGЃЌЧвEGЃКOGЃН2ЃЎЧѓжБЯпDEЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕуMЪЧЃЈ2ЃЉжажБЯпDEЩЯЕФвЛИіЖЏЕуЃЌдкxжсЩЯЗНЕФЦНУцФкЪЧЗёДцдкСэвЛЕуNЃЌЪЙвдOЁЂDЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыЧѓГіЕуNЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП
ЁО1ЁПШчЭМЃЌзїBHЁЭxжсЃЌДЙзуЮЊHЃЌФЧУДЫФБпаЮBCOHЮЊОиаЮЃЌOHЃНCBЃН3ЃЎ
дкRtЁїABHжаЃЌAHЃН3ЃЌBAЃН![]() ЃЌЫљвдBHЃН6ЃЎвђДЫЕуBЕФзјБъЮЊ(3,6)ЃЎ
ЃЌЫљвдBHЃН6ЃЎвђДЫЕуBЕФзјБъЮЊ(3,6)ЃЎ
ЁО2ЁПвђЮЊOEЃН2EBЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЌE(2,4)ЃЎ
ЃЌE(2,4)ЃЎ
ЩшжБЯпDEЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌДњШыD(0,5)ЃЌE(2,4)ЃЌ
ЕУ![]() НтЕУ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЎЫљвджБЯпDEЕФНтЮіЪНЮЊ
ЃЎЫљвджБЯпDEЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЁО3ЁПгЩ![]() ЃЌжЊжБЯпDEгыxжсНЛгкЕуF(10,0)ЃЌOFЃН10ЃЌDFЃН
ЃЌжЊжБЯпDEгыxжсНЛгкЕуF(10,0)ЃЌOFЃН10ЃЌDFЃН![]() ЃЎ
ЃЎ
ЂйШчЭМЃЌЕБDOЮЊСтаЮЕФЖдНЧЯпЪБЃЌMNгыDOЛЅЯрДЙжБЦНЗжЃЌЕуMЪЧDFЕФжаЕуЃЎ
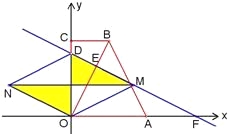
ДЫЪБЕуMЕФзјБъЮЊ(5,![]() )ЃЌЕуNЕФзјБъЮЊ(Ѓ5,
)ЃЌЕуNЕФзјБъЮЊ(Ѓ5,![]() )ЃЎ
)ЃЎ
ЂкШчЭМЃЌЕБDOЁЂDNЮЊСтаЮЕФСкБпЪБЃЌЕуNгыЕуOЙигкЕуEЖдГЦЃЌДЫЪБЕуNЕФзјБъЮЊ(4,8)ЃЎ
ЂлШчЭМЃЌЕБDOЁЂDMЮЊСтаЮЕФСкБпЪБЃЌNOЃН5ЃЌбгГЄMNНЛxжсгкPЃЎ
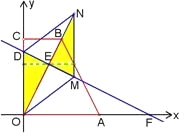
гЩЁїNPOЁзЁїDOFЃЌЕУ![]() ЃЌ
ЃЌ
МД![]() ЃЎ
ЃЎ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЎДЫЪБЕуNЕФзјБъЮЊ
ЃЎДЫЪБЕуNЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉзїBHЁЭxжсЃЌЙЙНЈОиаЮЃЌдкжБНЧШ§НЧаЮжаЧѓЕУBH=6ЃЌДгЖјЧѓЕУЕуBЕФзјБъЮЊ(3,6)ЁЃ
ЃЈ2ЃЉД§ЖЈЯЕЪ§ЗЈЧѓЕУжБЯпНтЮіЪНЁЃ
ЃЈ3ЃЉзлКЯадНЯЧПЃЌПМТЧШЋУцЪЧе§ШЗНтЬтЕФЙиМќЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌЁЯABCЃН45ЁуЃЌЕуDЮЊBCЕФжаЕуЃЌCEЁЭADгкЕуEЃЌЦфбгГЄЯпНЛABгкЕуFЃЌСЌНгDFЃЎЧѓжЄЃКЁЯADCЃНЁЯBDFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
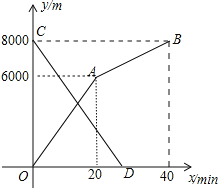
ЁОЬтФПЁПаЁУїКЭаЁССЗжБ№ДгМзЕиКЭввЕиЭЌЪБГіЗЂЃЌбиЭЌвЛЬѕТЗЯрЯђЖјааЃЌаЁУїПЊЪМХмВНЃЌжаЭОИФЮЊВНааЃЌЕНДяввЕиЧЁКУгУ![]() аЁССЦяздааГЕвд
аЁССЦяздааГЕвд![]() ЕФЫйЖШжБНгЕНМзЕиЃЌСНШЫРыМзЕиЕФТЗГЬ
ЕФЫйЖШжБНгЕНМзЕиЃЌСНШЫРыМзЕиЕФТЗГЬ![]() гыИїздРыПЊГіЗЂЕиЕФЪБМф
гыИїздРыПЊГіЗЂЕиЕФЪБМф![]() жЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌ
жЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌ
![]() МзЁЂввСНЕижЎМфЕФТЗГЬЮЊ______mЃЌаЁУїВНааЕФЫйЖШЮЊ______
МзЁЂввСНЕижЎМфЕФТЗГЬЮЊ______mЃЌаЁУїВНааЕФЫйЖШЮЊ______![]() ЃЛ
ЃЛ
![]() ЧѓаЁССРыМзЕиЕФТЗГЬyЙигкxЕФКЏЪ§БэДяЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЧѓаЁССРыМзЕиЕФТЗГЬyЙигкxЕФКЏЪ§БэДяЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
![]() ЧѓСНШЫЯргіЕФЪБМфЃЎ
ЧѓСНШЫЯргіЕФЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
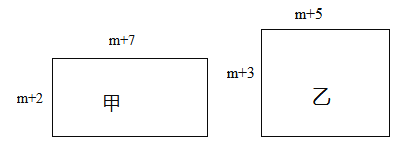
ЁОЬтФПЁПвбжЊгаМзЁЂввСНИіГЄЗНаЮЃЌЫќУЧЕФБпГЄШчЭМЫљЪОЃЈmЮЊе§ећЪ§ЃЉЃЌУцЛ§ЗжБ№ЮЊS1ЁЂS2ЃЎ
ЃЈ1ЃЉЧыБШНЯS1гыS2ЕФДѓаЁЃК S1ЁЁ ЁЁS2ЃЛ
ЃЈ2ЃЉШєвЛИіе§ЗНаЮгыМзЕФжмГЄЯрЕШЃЎ
ЂйЧѓИУе§ЗНаЮЕФБпГЄЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЂкШєИУе§ЗНаЮЕФУцЛ§ЮЊS3ЃЌЪдЬНОПЃКS3гыS1ЕФВюЃЈМДS3ЉS1ЃЉЪЧЗёЮЊГЃЪ§ЃПШєЮЊГЃЪ§ЃЌЧѓГіетИіГЃЪ§ЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєТњзуЬѕМў0ЃМnЃМ|S1ЉS2|ЕФећЪ§nгаЧвжЛга8ИіЃЌжБНгаДГіmЕФжЕВЂЗжБ№ЧѓГіS1гыS2ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСавЛзщЭМаЮжаЕуЕФИіЪ§ЃЌЦфжаЕк1ИіЭМжаЙВга4ИіЕуЃЌЕк2ИіЭМжаЙВга10ИіЕуЃЌЕк3ИіЭМжаЙВга19ИіЕуЃЌЁЃЌАДДЫЙцТЩЕк100ИіЭМжаЙВгаЕуЕФИіЪ§ЪЧ
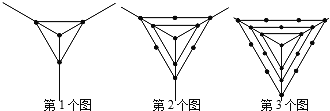
A. 15151B. 15152C. 15153D. 15154
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
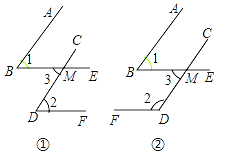
ЁОЬтФПЁПвбжЊвЛИіНЧЕФСНБпгыСэвЛИіНЧЕФСНБпЗжБ№ЦНааЃЌЧыНсКЯЭМЃЌЬНЫїетСНИіНЧжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌABЁЮCDЃЌBEЁЮDFЃЌЁЯ1гыЁЯ2ЕФЙиЯЕЪЧ ЃЛ
жЄУїЃК
ЃЈ2ЃЉШчЭМЂкЃЌABЁЮCDЃЌBEЁЮDFЃЌЁЯ1гыЁЯ2ЕФЙиЯЕЪЧ ЃЛ
жЄУїЃК
ЃЈ3ЃЉОЙ§ЩЯЪіжЄУїЃЌЮвУЧПЩЕУГіНсТлЃЌШчЙћвЛИіНЧЕФСНБпгыСэвЛИіНЧЕФСНБпЗжБ№ЦНааЃЌФЧУДетСНИіНЧ ЃЛ
ЃЈ4ЃЉШєетСНИіНЧЕФСНБпЗжБ№ЦНааЃЌЧввЛИіНЧБШСэвЛИіНЧЕФ3БЖЩй60ЁуЃЌдђетСНИіНЧЗжБ№ЪЧЖрЩйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧФГЭЌбЇЖдЖрЯюЪНЃЈx2Ѓ4x+2ЃЉЃЈx2Ѓ4x+6ЃЉ+4НјаавђЪНЗжНтЕФЙ§ГЬЃЎ
НтЃКЩшx2Ѓ4x=y
дЪН=ЃЈy+2ЃЉЃЈy+6ЃЉ+4 ЃЈЕквЛВНЃЉ
=y2+8y+16 ЃЈЕкЖўВНЃЉ
=ЃЈy+4ЃЉ2ЃЈЕкШ§ВНЃЉ
=ЃЈx2Ѓ4x+4ЃЉ2ЃЈЕкЫФВНЃЉ
ЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИУЭЌбЇЕкЖўВНЕНЕкШ§ВНдЫгУСЫвђЪНЗжНтЕФ_______ЃЎ
AЃЎЬсШЁЙЋвђЪН |
BЃЎЦНЗНВюЙЋЪН |
CЃЎСНЪ§КЭЕФЭъШЋЦНЗНЙЋЪН |
DЃЎСНЪ§ВюЕФЭъШЋЦНЗНЙЋЪН |
ЃЈ2ЃЉИУЭЌбЇвђЪНЗжНтЕФНсЙћЪЧЗёГЙЕзЃП________ЃЎЃЈЬюЁАГЙЕзЁБЛђЁАВЛГЙЕзЁБЃЉШєВЛГЙЕзЃЌЧыжБНгаДГівђЪНЗжНтЕФзюКѓНсЙћ_________ ЃЎ
ЃЈ3ЃЉЧыФуФЃЗТвдЩЯЗНЗЈГЂЪдЖдЖрЯюЪНЃЈx2Ѓ2xЃЉЃЈx2Ѓ2x+2ЃЉ+1НјаавђЪНЗжНтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЁЂЂкЁЂЂлЪЧШ§ИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЎ
ЃЈ1ЃЉШєЭЌЪБзЊЖЏЂйЁЂЂкСНИізЊХЬЃЌдђСНИізЊХЬЭЃЯТЪБжИеыЫљжИЕФЪ§зжЖМЪЧ2ЕФИХТЪЮЊЃЛ
ЃЈ2ЃЉМзЁЂввСНШЫгУШ§ИізЊХЬЭцгЮЯЗЃЌМззЊЖЏзЊХЬЃЌввМЧТМжИеыЭЃЯТЪБЫљжИЕФЪ§зжЃЎгЮЯЗЙцЖЈЃКЕБжИеыЫљжИЕФШ§ИіЪ§зжжагаЪ§зжЯрЭЌЪБЃЌОЭЫуМзгЎЃЌЗёдђОЭЫуввгЎЃЎЧыХаЖЯетИігЮЯЗЪЧЗёЙЋЦНЃЌВЂЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com