练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知α、β是一元二次方程x2﹣4x﹣1＝0的两实数根，则代数式（α﹣2）（β﹣2）＝____.

    【答案】﹣5．

    【解析】

    先根据根与系数的关系得到α+β和αβ的值，再把（α-2）（β-2）展开整理为αβ-2（α+β）+4，然后利用整体思想代入计算即可．

    解：根据题意得α+β＝4，αβ＝﹣1，

    所以原式＝αβ﹣2（α+β）+4

    ＝﹣1﹣2×4+4

    ＝﹣1﹣8+4

    ＝﹣5．

    故答案为﹣5．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】请根据图中提供的信息，回答下列问题：

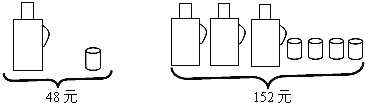
    一个水瓶与一个水杯分别是多少元？

    （2）甲、乙两家商场同时出售同样的水瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打八折；乙商场规定：买一个水瓶赠送两个水杯，另外购买的水杯按原价卖．若某单位想要买5个水瓶和20个水杯，请问选择哪家商场购买更合算，并说明理由．（必须在同一家购买）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

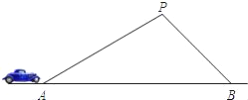
    【题目】某条道路上通行车辆限速为60千米/时，在离道路50米的点P处建一个监测点，道路AB段为检测区（如图）．在△ABP中，已知∠PAB=30°，∠PBA=45°，一辆轿车通过AB段的时间8.1秒，请判断该车是否超速？（参考数据： ≈1.41， ≈1.73，60千米/时=米/秒）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知甲队有x人，乙队有y人，若从甲队调出10人到乙队，则乙队人数是甲队人数的2倍，调整后两队人数间的数量关系用等式表示为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在弹簧限度内，弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表：

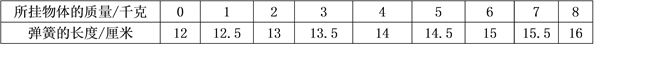
    （1）上表中，自变量是 ，因变量是 ；

    （2）弹簧不挂物体的长度是 ；

    （3）如果用x表示弹性限度内物体的质量，用y表示弹簧的长度，那么随着x的变化，y的变化趋势是 ，写出y与x的关系式 ；

    （4）如果弹簧最大挂质量为25千克，你能计算出当挂重为14千克时，弹簧的长度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若2x3﹣2k+2k＝41是关于x的一元一次方程，则k＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把Rt△ACO以O点为中心，逆时针旋转90 ，得Rt△BDO，点B坐标为（0，-3），点C坐标为（0， ），，抛物线y=-x2+bx+c经过点A和点C
    （1）求b，c的值；
    （2）在x轴以上的抛物线对称轴上是否存在点Q，使得△ACQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由
    （3）点P从点O出发沿ｘ轴向负半轴运动，每秒1个单位，过点P作y轴的平行线交抛物线于点M，当ｔ为几秒时，以M、P、O、C为顶点得四边形是平行四边形？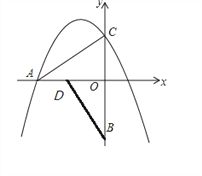

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里，据预测，海鲜的市场价格将每天每千克上涨1元．冷冻存放这批海鲜每天需要支出各种费用合计310元，而且这些海鲜在冷库中最多存放160天，同时平均每天有3千克的海鲜变质．
    （1）设x天后每千克该海鲜的市场价格为y元，试写出y与x之间的函数关系式；
    （2）若存放x天后，将这批海鲜一次性出售．设这批海鲜的销售总额为P元，试写出P与x之间的函数关系式；
    （3）小李将这批海鲜存放多少天后出售可获得最大利润，最大利润是多少元？（利润W=销售总额﹣收购成本﹣各种费用）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

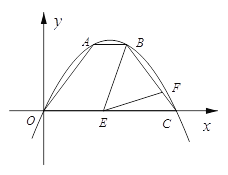
    【题目】如图，一条抛物线经过原点和点C（8，0），A、B是该抛物线上的两点，AB∥x轴，点A坐标为（3，4），点E在线段OC上，点F在线段BC上，且满足∠BEF=∠AOC.

    （1）求抛物线的解析式；

    （2）若四边形OABE的面积为14，求S△ECF；

    （3）是否存在点E，使得△BEF为等腰三角形？若存在，求点E的坐标；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案