
【题目】在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a= ![]() ,∠A=60°,求b、c.
,∠A=60°,求b、c.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G. 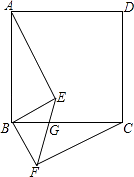
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数![]() 排列成如图所示得一个数表.
排列成如图所示得一个数表.
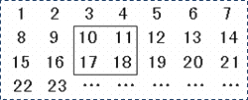
⑴用一个正方形在表中随意框住4个数,把其中最小的数记为![]() ,另外三个数用含
,另外三个数用含![]() 的式子表示出来,从大到小依次是 _____ ,_______ ,________ ;
的式子表示出来,从大到小依次是 _____ ,_______ ,________ ;
⑵.当被框住的4个数之和等于416时, ![]() 的值是多少?
的值是多少?
⑶被框住的4个数之和能否等于622?如果能,请求出![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 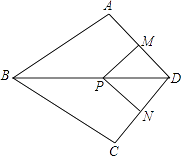
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC. 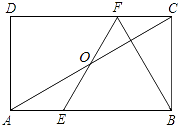
(1)求证:OE=OF;
(2)若BC=2 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,电器商社从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)电器商社决定用不超过14000元从厂家购进A,B两种型号的空气净化器共10台,且B型空气净化器的台数少于A型空气净化器的台数的2倍,问电器商社有几种进货方案?如果两种型号的空气净化器在进价的基础上都加价50%销售,请你在上述方案中选一个方案使得电器商社在销售完10台空气净化器能获得最多利润.
(3)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,电器商社决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天电器商社销售B型空气净化器的利润为3200元,请问电器商社应将B型空气净化器的售价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com