
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 内含 |
分析 此题首先应求得圆心到直线的距离,根据直角三角形的面积公式即可求得;再进一步根据这些和圆的位置关系与数量之间的联系进行判断.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 解:∵BC=6厘米,AC=8厘米,
∴AB=$\sqrt{{6}^{2}{+8}^{2}}$=10,S△ABC=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×6×8=24,
∴AB上的高为:24×2÷10=4.8,
即圆心到直线的距离是4.8,
∵4.8<5,
∴直线和圆相交.
故选C.
点评 本题主要考查了直线与圆的位置关系,根据三角形的面积求出斜边上的高的长度是解答此题关键.
注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.


科目:初中数学 来源: 题型:填空题
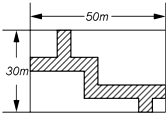 如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.
如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
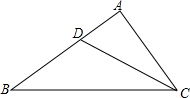 如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).
如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
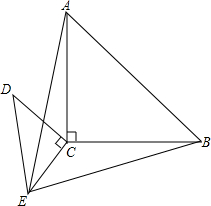 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.
在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
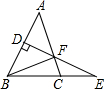 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )| A. | 16cm,40° | B. | 8cm,50° | C. | 16cm,50° | D. | 8cm,40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com