
【题目】如图所示.在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
①分别用外角减去内角表示∠ACB和∠APB,即可得到结论;
②根据角平分线的性质和三角形的面积公式即可求出结论;
③根据线段垂直平分线的性质即可得结果;
④根据角平分线的性质和平行线的性质即可得到结果.
①∠ACB=∠CBE-∠CAB=2∠PBE-2∠PAB=2(∠PBE-∠PAB)=2∠APB.
②∵AP平分∠BAC,
∴P到AC,AB的距离相等,
∴S△PAC:S△PAB=AC:AB,
③∵BE=BC,BP平分∠CBE,
∴BP垂直平分CE(三线合一),
④∵∠BAC与∠CBE的平分线相交于点P,可得点P也位于∠BCD的平分线上,
∴∠DCP=∠BCP,
又∵PG∥AD,
∴∠FPC=∠DCP,
故①②③④都正确.
故答案选:D.


科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D. 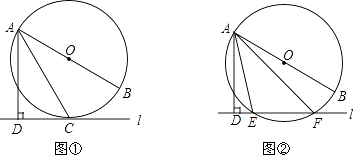
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次军事演习中,蓝方在﹣条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
(1)求点C到公路的距离;
(2)求红蓝双方最初的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC.
(1)用直尺和圆规作∠A的平分线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() ;
;
(要求:不写作法,但需要保留画图痕迹)
(2)设(1)中的![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请你探究BE和CF之间的数量关系,并加以证明.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请你探究BE和CF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上,![]() ,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com