
【题目】如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
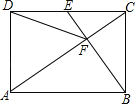
A. △ADC∽△CFBB. AD=DF
C. ![]() D.
D. ![]() =
=![]()
【答案】C
【解析】
依据∠ADC=∠CFB=90°,∠CAD=∠BCF,即可得到△ADC∽△CFB;过D作DM∥BE交AC于N,交AB于M,得出DM垂直平分AF,即可得到DF=DA;设CE=a,AD=b,则CD=2a,由△ADC∽△CFB,可得![]() =
=![]() ,可得b=
,可得b=![]() a,依据
a,依据![]() 即可得出
即可得出![]() ,根据E是CD边的中点,可得CE:AB=1:2,再根据△CEF∽△ABF,即可得到
,根据E是CD边的中点,可得CE:AB=1:2,再根据△CEF∽△ABF,即可得到![]() =(
=(![]() )2=
)2=![]() .
.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=∠BCD=90°,
∴∠CAD=∠BCF,
∵BE⊥AC,
∴∠CFB=90°,
∴∠ADC=∠CFB,
∴△ADC∽△CFB,故A选项正确;
如图,过D作DM∥BE交AC于N,交AB于M,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() DC,
DC,
∴BM=AM,
∴AN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥AF,
∴DM垂直平分AF,
∴DF=DA,故B选项正确;
设CE=a,AD=b,则CD=2a,
由△ADC∽△ECB,可得![]() =
=![]() ,
,
即b=![]() a,
a,
∴![]()
∴![]() ,故C选项错误;
,故C选项错误;
∵E是CD边的中点,
∴CE:AB=1:2,
又∵CE∥AB,
∴△CEF∽△ABF,
∴![]() =(
=(![]() )2=
)2=![]() .
.
故选D选项正确;
故选:C.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a≠0)经过点A(6,﹣3),对称轴是直线x=4,顶点为B,OA与其对称轴交于点M,M、N关于点B对称.
(1)求这条抛物线的表达式和点B的坐标;
(2)联结ON、AN,求△OAN的面积;
(3)点Q在x轴上,且在直线x=4右侧,当∠ANQ=45°时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
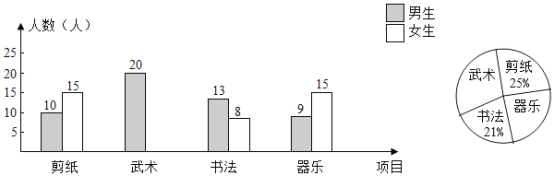
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的快速发展,人们对生活质量的要求越来越高,净水器已经走入普通百姓家庭.某电器公司销售A、B两种型号的净水器,第一周售出A型号净水器4台,B型号净水器5台,收人20500元.第二周售出A型号净水器6台,B型号净水器10台,收人36000元.
(1)求A、B两种型号的净水器的销售单价;
(2)若该电器公司计划第三周销售这两种型号净水器20台,要使销售收入不低于45000元,则第三周至少要售出A种型号的净水器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
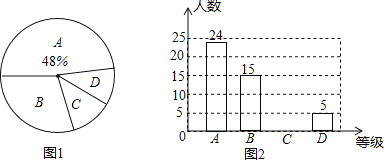
【题目】某销售公司年终进行业绩考核,人事部门把考核结果按照A,B,C,D四个等级,绘制成两个不完整的统计图,如图1,图2.
![]() 参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
![]() 若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
![]() 为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率
为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率![]() 精确到
精确到![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
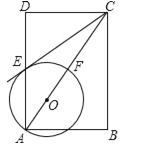
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
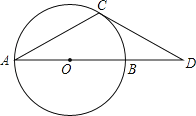
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,
①用尺规作出点A到CD所在直线的距离;
②求出该距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
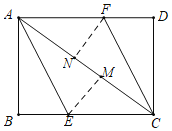
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当∠BAE为多少度时,四边形AECF是菱形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com