
ЁОЬтФПЁПЫцзХЩчЛсЕФПьЫйЗЂеЙЃЌШЫУЧЖдЩњЛюжЪСПЕФвЊЧѓдНРДдНИпЃЌОЛЫЎЦївбОзпШыЦеЭЈАйаеМвЭЅЃЎФГЕчЦїЙЋЫОЯњЪлAЁЂBСНжжаЭКХЕФОЛЫЎЦїЃЌЕквЛжмЪлГіAаЭКХОЛЫЎЦї4ЬЈЃЌBаЭКХОЛЫЎЦї5ЬЈЃЌЪеШЫ20500дЊЃЎЕкЖўжмЪлГіAаЭКХОЛЫЎЦї6ЬЈЃЌBаЭКХОЛЫЎЦї10ЬЈЃЌЪеШЫ36000дЊЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЃЛ
ЃЈ2ЃЉШєИУЕчЦїЙЋЫОМЦЛЎЕкШ§жмЯњЪлетСНжжаЭКХОЛЫЎЦї20ЬЈЃЌвЊЪЙЯњЪлЪеШыВЛЕЭгк45000дЊЃЌдђЕкШ§жмжСЩйвЊЪлГіAжжаЭКХЕФОЛЫЎЦїЖрЩйЬЈЃП
ЁОД№АИЁПЃЈ1ЃЉAЁЂBСНжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЗжБ№ЮЊ2500дЊ/ЬЈЃЌ2100дЊ/ЬЈЃЛЃЈ2ЃЉЕкШ§жмжСЩйвЊЪлГіAжжаЭКХЕФОЛЫЎЦї8ЬЈЃЛ
ЁОНтЮіЁП
ЩшAжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЮЊxдЊ/ЬЈЃЌBжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЮЊyдЊ/ЬЈЃЌСаГіЗНГЬзщНтЗНГЬзщМДПЩЃЌЕкЖўЮЪЩшЯњЪлAжжаЭКХЕФОЛЫЎЦїmЬЈЃЌдђЯњЪлBжжаЭКХЕФОЛЫЎЦїЃЈ20ЉmЃЉЬЈЃЌСаГіВЛЕШЪННтВЛЕШЪНМДПЩ
НтЃКЃЈ1ЃЉAжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЮЊxдЊ/ЬЈЃЌBжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЮЊyдЊ/ЬЈЃЌ
ИљОнЬтвтЕУЃК![]()
НтЕУЃК![]()
Д№ЃКAЁЂBСНжжаЭКХЕФОЛЫЎЦїЕФЯњЪлЕЅМлЗжБ№ЮЊ2500дЊ/ЬЈЃЌ2100дЊ/ЬЈЃЌ
ЃЈ2ЃЉЩшЯњЪлAжжаЭКХЕФОЛЫЎЦїmЬЈЃЌдђЯњЪлBжжаЭКХЕФОЛЫЎЦїЃЈ20ЉmЃЉЬЈ
ИљОнЬтвтЕУЃК2500m+2100ЃЈ20ЉmЃЉЁн45000
НтЕУЃКmЁн7![]()
ЧвmШЁе§ећЪ§ЃЌ
ЁрзюаЁжЕЮЊ8
Д№ЕкШ§жмжСЩйвЊЪлГіAжжаЭКХЕФОЛЫЎЦї8ЬЈ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3ЃЌEЮЊADЕФжаЕуЃЌFЮЊCDЩЯвЛЕуЃЌЧвDFЃН2CFЃЌбиBEНЋЁїABEЗелЃЌШчЙћЕуAЧЁКУТфдкBFЩЯЃЌдђADЃН_ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
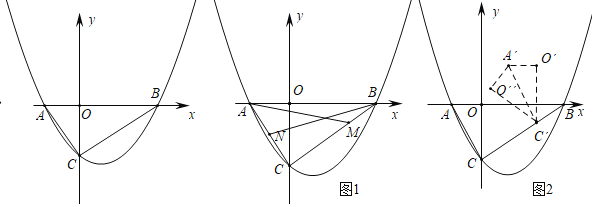
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНax2+bx+cгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉКЭBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌСЌНгACЁЂBCЃЌЧвЁЯACBЃН90ЁуЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЈ1ЃЉЃЌШєNЪЧACЕФжаЕуЃЌMЪЧBCЩЯвЛЕуЃЌЧвТњзуCMЃН2BMЃЌСЌAMЁЂBNЯрНЛгкЕуEЃЌЧѓЕуMЕФзјБъКЭЁїEMBЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМЃЈ2ЃЉЃЌНЋЁїAOCбижБЯпBCЦНвЦЕУЕНЁїAЁфOЁфCЁфЃЌдйНЋЁїAЁфOЁфCЁфбиAЁфCЁфЗелЕУЕНЁїAЁфOЁфCЁфЃЌСЌНгAOЁфЃЌACЁфЃЌЧыЮЪЁїAOЁфCЁфФмЗёЙЙГЩЕШбќШ§НЧаЮЃПШєФмЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуCЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
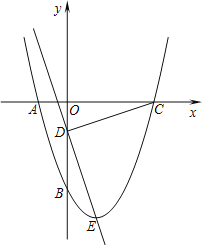
ЁОЬтФПЁПШчЭМЫљЪОЃЌХзЮяЯпy=x2+bx+cОЙ§AЁЂBСНЕуЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕуEЮЊХзЮяЯпЕФЖЅЕуЃЌЕуCЮЊХзЮяЯпгыxжсЕФСэвЛНЛЕуЃЌЕуDЮЊyжсЩЯвЛЕуЃЌЧвDC=DEЃЌЧѓГіЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЕкЖўЮЪЕФЬѕМўЯТЃЌдкжБЯпDEЩЯДцдкЕуPЃЌЪЙЕУвдCЁЂDЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїDOCЯрЫЦЃЌЧыФужБНгаДГіЫљгаТњзуЬѕМўЕФЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCЃЌABЃНACЃЌDЮЊжБЯпBCЩЯвЛЕуЃЌEЮЊжБЯпACЩЯвЛЕуЃЌADЃНAEЃЌЩшЁЯBADЃНІСЃЌЁЯCDEЃНІТЃЌ
ЃЈ1ЃЉШчЭМ1ЃЌШєЕуDдкЯпЖЮBCЩЯЃЌЕуEдкЯпЖЮACЩЯЃЎЁЯABCЃН60ЁуЃЌЁЯADEЃН70ЁуЃЌдђІСЃНЁЁ ЁЁЁуЃЛІТЃНЁЁ ЁЁЁуЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуDдкЯпЖЮBCЩЯЃЌЕуEдкЯпЖЮACЩЯЃЌдђІСЃЌІТжЎМфгаЪВУДЙиЯЕЪНЃПЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЪЧЗёДцдкВЛЭЌгкЃЈ2ЃЉжаЕФІСЃЌІТжЎМфЕФЙиЯЕЪНЃПШєДцдкЃЌЧыаДГіетИіЙиЯЕЪНЃЈаДГівЛжжМДПЩЃЉЃЌЫЕУїРэгЩЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
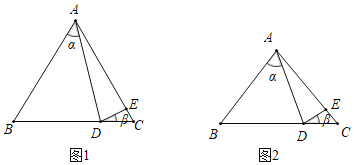
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌEЪЧCDБпЕФжаЕуЃЌЧвBEЁЭACгкЕуFЃЌСЌНгDFЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
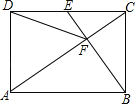
A. ЁїADCЁзЁїCFBB. ADЃНDF
C. ![]() D.
D. ![]() ЃН
ЃН![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуCЃЈ0ЃЌ3ЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊAЃЈ2ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЈ0ЃЌ1ЃЉЃЌFдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвзнзјБъЮЊ1ЃЎЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPMЁЭxжсгкЕуMЃЌНЛжБЯпCFгкЕуHЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPдкжБЯпCFЯТЗНЕФХзЮяЯпЩЯЃЌгУКЌmЕФДњЪ§ЪНБэЪОЯпЖЮPHЕФГЄЃЌВЂЧѓГіЯпЖЮPHЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕБPFЉPMЃН1ЪБЃЌШєНЋЁАЪЙЁїPCFУцЛ§ЮЊ2ЁБЕФЕуPМЧзїЁАЧЩЕуЁБЃЌдђДцдкЖрИіЁАЧЩЕуЁБЃЌЧвЪЙЁїPCFЕФжмГЄзюаЁЕФЕуPвВЪЧвЛИіЁАЧЩЕуЁБЃЌЧыжБНгаДГіЫљгаЁАЧЩЕуЁБЕФИіЪ§ЃЌВЂЧѓГіЁїPCFЕФжмГЄзюаЁЪБЁАЧЩЕуЁБЕФзјБъЃЎ
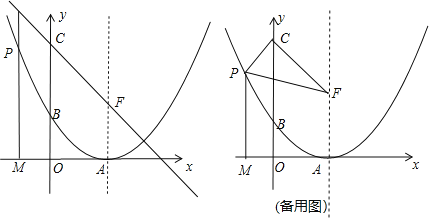
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
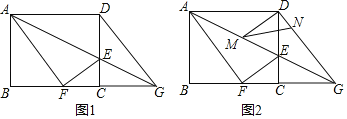
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЌBЃЌCЃЌDЫФЕуЕФзјБъвРДЮЮЊЃЈ0ЃЌ0ЃЉЃЌЃЈ6ЃЌ2ЃЉЃЌЃЈ8ЃЌ8ЃЉЃЌЃЈ2ЃЌ6ЃЉЃЌШєвЛДЮКЏЪ§yЃНmxЉ6m+2ЃЈmЁй0ЃЉЭМЯѓНЋЫФБпаЮABCDЕФУцЛ§ЗжГЩ1ЃК3СНВПЗжЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. Љ4B. ![]() ЃЌЉ5C.
ЃЌЉ5C. ![]() D.
D. ![]() ЃЌЉ4
ЃЌЉ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЌСЌНг
БпЩЯвЛЕуЃЌСЌНг![]() ЃЌНЋОиаЮ
ЃЌНЋОиаЮ![]() би
би![]() елЕўЃЌЖЅЕу
елЕўЃЌЖЅЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() БпЩЯЕу
БпЩЯЕу![]() ДІЃЌбгГЄ
ДІЃЌбгГЄ![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧЯпЖЮ
ЗжБ№ЪЧЯпЖЮ![]() ЃЌ
ЃЌ![]() ЩЯЕФЖЏЕуЃЈгыЖЫЕуВЛжиКЯЃЉЃЌЧв
ЩЯЕФЖЏЕуЃЈгыЖЫЕуВЛжиКЯЃЉЃЌЧв![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйаДГі![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГі
ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГі![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ЂкЪЧЗёДцдкетбљЕФЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГі
ЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com