
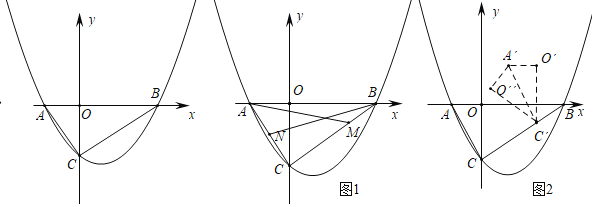
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��ax2+bx+c��x���ཻ�ڵ�A����1��0����B��3��0������y�ύ�ڵ�C������AC��BC���ҡ�ACB��90����
��1������κ����Ľ���ʽ��
��2����ͼ��1������N��AC���е㣬M��BC��һ�㣬������CM��2BM����AM��BN�ཻ�ڵ�E�����M���������EMB�������
��3����ͼ��2��������AOC��ֱ��BCƽ�Ƶõ���A��O��C�����ٽ���A��O��C����A��C�����۵õ���A��O��C��������AO����AC����������AO��C���ܷɵ��������Σ����ܣ���������з��������ĵ�C�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��C��������
����3��C��������![]() ����
����![]() ��
��![]() ����
����![]() ����
����
��������
��1����ACB��90�㣬��OC2��OA��OB��3�����C��0����![]() ����������⣻
����������⣻
��2��֤����S��BEM��S��![]() S��ABM��������⣻
S��ABM��������⣻
��3����O��C�䣽AO�塢O��C�䣽AC�䡢AO�壽AC�䣬����������ֱ���⼴�ɣ�
�⣺��1���ߡ�ACB��90����
��OBC+��OCB��90������ACO+��BCO��90�������OBC����ACO��
���COB�ס�AOC����OC2��OA��OB��3��
���C��0����![]() �������ACO��30����
�������ACO��30����
����κ�������ʽΪ��y��a��x+1����x��3����a��x2��2x��3����
������3a����![]() ����a��
����a��![]() ��
��
�������ߵı���ʽΪ��![]() ��
��
��2����C��0����![]() ������B��0��3����
������B��0��3����
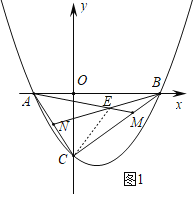
��CM��2BM����M��2��![]() ����
����
����CE������N��AC���е㣬
��S��ABN��S��CBN��S��AEN��S��CEN��
��S��EBA��S��EBC��
�裺S��BEM��S����CM��2BM��S��CBE��3S��S��EBA��
��S��BEM��S��![]() S��ABM��
S��ABM��![]() ��
��![]() ��
��
��3���ܣ����ɣ�
��ͼ2������C����x���ƽ���߽�����O����y���ƽ�����ڵ�H��
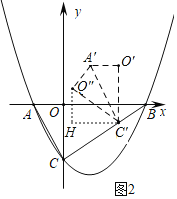
�ߡ�AOC��30�������O��C��H��30����������HC��O����90����
����B��C���������һ�κ�������ʽ��y��kx+b����ã�
ֱ��BC�ı���ʽΪ��![]() ��
��
���C����n��![]() ������HC����C��O��cos30����
������HC����C��O��cos30����![]() ��
��
HO����![]() �����O����
�����O����![]() ��
��![]() ����
����
��O��C��2��3��AO��2��![]() +
+![]() 2��AC��2����n+1��2+
2��AC��2����n+1��2+![]()
�ٵ�O��C����AO��ʱ��3��![]() +
+![]() ����ã�
����ã�![]() ��
��
�ڵ�O��C����AC��ʱ���⣻
�۵�AO����AC��ʱ��ͬ���ɵã�![]() ��
��
�ʵ�C������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB��![]() ��BC��6����B��45����DΪBC����һ�㽫��ABC���Ź�D���ֱ���۵���ʹ�õ�C����AB���ϣ���CD��m����AC��_____��m��ȡֵ��Χ��_____
��BC��6����B��45����DΪBC����һ�㽫��ABC���Ź�D���ֱ���۵���ʹ�õ�C����AB���ϣ���CD��m����AC��_____��m��ȡֵ��Χ��_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
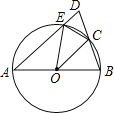
����Ŀ����ͼ���ڡ�ABD�У�AB��AD��AB����O��ֱ����DA��DB�ֱ���O�ڵ�E��C������EC��OE��OC��
��1������BAD�����ʱ����֤����OBC�ա�OEC��
��2����գ�
����AB��2�����AOE���������� ��
����DA����O����ʱ����AB��![]() ����AC�ij�Ϊ�� ��
����AC�ij��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
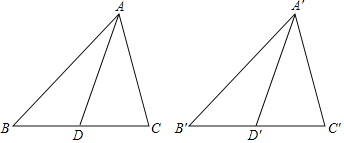
����Ŀ����֪����ͼ������ABC����A'B'C'�У�AD��A'D'�ֱ�����ABC����A'B'C'�����ߣ�AB��A'B'��BC��B'C'��AD��A'D'����֤����ABC�ա�A'B'C'��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
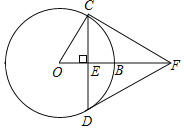
����Ŀ����ͼ����B�ǡ�O��һ�㣬��CD��OB�ڵ�E������C�����߽�OB���ӳ����ڵ�F������DF��
��1����֤��DF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2����CFD��60������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㴫ͳ�Ļ���У����У�ѧУ�ƻ�ÿ�ܶ���������ڿ�ʱ�俪չ�������չ���ĿΪ����ֽ���������鷨�����֣�Ҫ�����꼶ѧ�����˲μӣ�����ÿ��ֻ�ܲμ�����һ���������ڸ�У���꼶ѧ���������ȡ��100��ѧ�����е��飬���Դ˽���ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������������
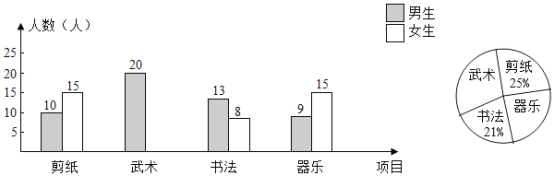
�����������⣺
��1���벹ȫ����ͳ��ͼ������ͳ��ͼ��
��2���ڲμ�����ֽ�����Ŀ��ѧ���У�������ռ�İٷֱ��Ƕ��٣�
��3������У���꼶ѧ������500�ˣ���������вμ����鷨����Ŀ����ж����ˣ�
��4��ѧУ����Ҫ����Щ�������Ů���У������ȡһ���˽�����������ô���ó鵽�μ������������Ŀ��Ů���ĸ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������.
A. �����ӻ������ڲ��š��������硷���DZ�Ȼ�¼�
B. ij�ֲ�Ʊ���н�����Ϊ![]() ��˵��ÿ��1000�ţ�һ����һ���н�
��˵��ÿ��1000�ţ�һ����һ���н�
C. ����һö�ʵؾ��ȵ�Ӳ��һ�Σ��������泯�ϵĸ���Ϊ![]()
D. ���˽ⳤɳ�����г��������˾�������ˮƽ���˲��ó�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ŀ��ٷ�չ�����Ƕ�����������Ҫ��Խ��Խ�ߣ���ˮ���Ѿ�������ͨ���ռ�ͥ��ij������˾����A��B�����ͺŵľ�ˮ������һ���۳�A�ͺž�ˮ��4̨��B�ͺž�ˮ��5̨������20500Ԫ���ڶ����۳�A�ͺž�ˮ��6̨��B�ͺž�ˮ��10̨������36000Ԫ��
��1����A��B�����ͺŵľ�ˮ�������۵��ۣ�
��2�����õ�����˾�ƻ������������������ͺž�ˮ��20̨��Ҫʹ�������벻����45000Ԫ�������������Ҫ�۳�A���ͺŵľ�ˮ������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
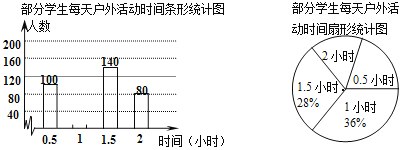
����Ŀ��Ϊ�˽�ѧ���μӻ����������ij�н����������ŶԲ���ѧ���μӻ�����ʱ������˳������飬�������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1����γ������������� ��ѧ��������ȫ����ͳ��ͼ��
��2����������ͳ��ͼ�б�ʾ����ʱ��0.5Сʱ������Բ�ĽǶ�����
��3��������ε���ѧ���μӻ�����ƽ��ʱ�䣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com