
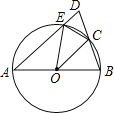
【题目】如图,在△ABD中,AB=AD,AB是⊙O的直径,DA、DB分别交⊙O于点E、C,连接EC,OE,OC.
(1)当∠BAD是锐角时,求证:△OBC≌△OEC;
(2)填空:
①若AB=2,则△AOE的最大面积为 ;
②当DA与⊙O相切时,若AB=![]() ,则AC的长为 .
,则AC的长为 .
【答案】(1)见解析;(2)①S△AOE最大=![]() ;②AC=1.
;②AC=1.
【解析】
(1)利用垂直平分线,判断出∠BAC=∠DAC,得出EC=BC,用SSS判断出结论;
(2)①先判断出三角形AOE面积最大,只有点E到直径AB的距离最大,即是圆的半径即可;②根据切线的性质和等腰直角三角形的性质解答即可.
(1)连接AC,如图1,
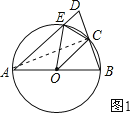
∵AB是⊙O的直径,
∴AC⊥BD,
∵AD=AB,
∴∠BAC=∠DAC,
∴![]() ,
,
∴BC=EC,
在△OBC和△OEC中 ,
,
∴△OBC≌△OEC(SSS),
(2)①∵AB是⊙O的直径,且AB=2,
∴OA=1,
设△AOE的边OA上的高为h,
∴S△AOE=![]() OA×h=
OA×h=![]() ×1×h=
×1×h=![]() h,
h,
∴要使S△AOE最大,只有h最大,
∵点E在⊙O上,
∴h最大是半径,
即h最大=1
∴S△AOE最大=![]() ,
,
故答案为![]() ;
;
②如图2:
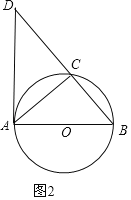
当DA与⊙O相切时,
∴∠DAB=90°,
∵AD=AB=![]() ,
,
∴∠ABD=45°,
∵AB是直径,
∴∠ADB=90°,
∴AC=BC=![]() ,
,
故答案为1


科目:初中数学 来源: 题型:
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东67°方向,距离B地520km,C地位于A地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
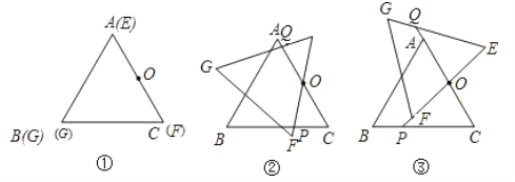
【题目】△ABC和△EFG是两块完全重合的等边三角形纸片,(如图①所示)O是AB(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α﹝0°<α<120°﹞角.
(1)试分别说明α为多少度时,点F在△ABC外部、BC上、内部(不证明)?
(2)当点F不在BC上时,在图②、图③两种情况下(设EF或延长线与BC交于P,EG与CA或延长线交于Q),分别写出OP与OQ的数量关系,并将图③情况给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
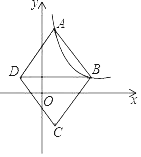
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,点A、B横坐标分别为2和6,对角线BD∥x轴,若菱形ABCD的面积为40,则k的值为( )
(k>0,x>0)的图象上,点A、B横坐标分别为2和6,对角线BD∥x轴,若菱形ABCD的面积为40,则k的值为( )
A.15B.10C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某县政府部门决定,招标一工程队负责完成一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米.每台A型挖掘机一个小时的施工费用是350元,每台B型挖掘机一个小时的施工费用是200元.
(1)分别求每台A型,B型挖掘机一小时各挖土多少立方米?
(2)若A型和B型挖掘机共10台同时施工4小时,至少完成1360立方米的挖土量,且总费用不超过14000元.问施工时有哪几种调配方案?且指出哪种调配方案的施工费用最低,最低费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购进一批新产品进行销售,已知该产品的进货单价为8元/件,该公司对这批新产品上市后的销售情况进行了跟踪调查.销售过程中发现,该产品每月的销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系满足下表.
(元)之间的关系满足下表.
销售单价 | … | 10 | 12 | 14 | 15 | … |
每月销售量 | … | 40 | 36 | 32 | 30 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当销售单价为多少元时,该产品每月获得的利润为240万元?
(3)如果该产品每月的进货成本不超过160万元,那么当销售单价为多少元时,该产品每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com