
����Ŀ����֪��ABC��AB��AC��DΪֱ��BC��һ�㣬EΪֱ��AC��һ�㣬AD��AE�����BAD��������CDE������
��1����ͼ1������D���߶�BC�ϣ���E���߶�AC�ϣ���ABC��60������ADE��70������������ ������������ ������
��2����ͼ2������D���߶�BC�ϣ���E���߶�AC�ϣ���������֮����ʲô��ϵʽ��˵�����ɣ�
��3���Ƿ���ڲ�ͬ�ڣ�2���е�������֮��Ĺ�ϵʽ�������ڣ���д�������ϵʽ��д��һ�ּ��ɣ���˵�����ɣ��������ڣ���˵�����ɣ�
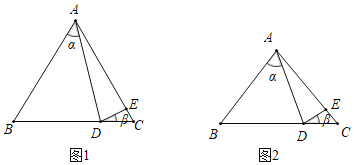
���𰸡���1��20��10����2������2�£���3��������.
��������
��1�������õ��������ε����������DAE�����������BAD�����ɵó����ۣ�
��2�����õ��������ε����ʺ������ε��ڽǺͼ��ɵó����ۣ�
��3���ٵ���E��CA���ӳ����ϣ���D���߶�BC�ϣ�ͬ��1���ķ������ɵó����ۣ�
�ڵ���E��CA���ӳ����ϣ���D��CB���ӳ����ϣ�ͬ��1���ķ������ɵó����ۣ�
��1����AB=AC����ABC=60����
���BAC=60����
��AD=AE����ADE=70����
���DAE=180����2��ADE=40����
����=��BAD=60����40��=20����
���ADC=��BAD+��ABD=60��+20��=80����
����=��CDE=��ADC����ADE=10����
�ʴ�Ϊ��20��10��
��2�����ABC=x����AED=y��
���ACB=x����AED=y��
����DEC��y=��+x��
����ABD����+x=y+��=��+x+����
����=2����
��3���ٵ���E��CA���ӳ����ϣ���D���߶�BC�ϣ�
��ͼ1
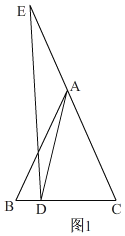
���ABC=x����ADE=y��
���ACB=x����ACE=y��
����ABD��x+��=����y��
����DEC��x+y+��=180����
����=2����180����
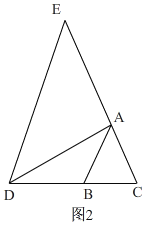
�ڵ���E��CA���ӳ����ϣ���D��CB���ӳ����ϣ�
��ͼ2��ͬ�ٵķ����ɵ���=180����2����


 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ֱ���ij��ȫ��ѧ����ѧʱ�˳������С��ﳵ�����ķֲ�ֱ��ͼ������ͳ��ͼ����ͼ���������������н��۴�����ǣ� ��

A. �ð�������Ϊ50��B. ��������Ϊ30��
C. �˳��������ﳵ������2.5��D. �ﳵ����ռ20%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
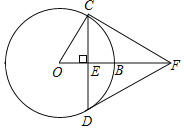
����Ŀ����ͼ����B�ǡ�O��һ�㣬��CD��OB�ڵ�E������C�����߽�OB���ӳ����ڵ�F������DF��
��1����֤��DF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2����CFD��60������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������.
A. �����ӻ������ڲ��š��������硷���DZ�Ȼ�¼�
B. ij�ֲ�Ʊ���н�����Ϊ![]() ��˵��ÿ��1000�ţ�һ����һ���н�
��˵��ÿ��1000�ţ�һ����һ���н�
C. ����һö�ʵؾ��ȵ�Ӳ��һ�Σ��������泯�ϵĸ���Ϊ![]()
D. ���˽ⳤɳ�����г��������˾�������ˮƽ���˲��ó�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ����������ë�������������·ֱ���A��B��C��D��ʾ�������������˶���ϲ���������ȫ��ѧ�������˳������飨ÿλѧ��ֻ��ѡһ����ϲ�����˶�������������������Ƴ�����������������ͳ��ͼ��
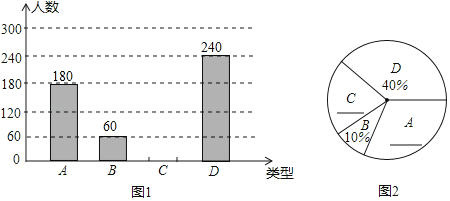
�����������Ϣ�ش��������⣺
��1�����βμӳ��������ѧ������ ���ˣ�
��2����ȫ����ͳ��ͼ��
��3�����ӱ��βμӳ��������ѧ������ȡ1�ˣ������ϲ��������ĸ������������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ŀ��ٷ�չ�����Ƕ�����������Ҫ��Խ��Խ�ߣ���ˮ���Ѿ�������ͨ���ռ�ͥ��ij������˾����A��B�����ͺŵľ�ˮ������һ���۳�A�ͺž�ˮ��4̨��B�ͺž�ˮ��5̨������20500Ԫ���ڶ����۳�A�ͺž�ˮ��6̨��B�ͺž�ˮ��10̨������36000Ԫ��
��1����A��B�����ͺŵľ�ˮ�������۵��ۣ�
��2�����õ�����˾�ƻ������������������ͺž�ˮ��20̨��Ҫʹ�������벻����45000Ԫ�������������Ҫ�۳�A���ͺŵľ�ˮ������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������y�T![]() ��x��0����һ�㣬����A��AB��x���ڵ�B����ABΪ�������Ҳ���������ABCD������A��˫����y��
��x��0����һ�㣬����A��AB��x���ڵ�B����ABΪ�������Ҳ���������ABCD������A��˫����y��![]() ��CD���ڵ�E����
��CD���ڵ�E����![]() ��ֵΪ_____��
��ֵΪ_____��
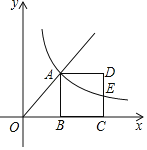
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ȫУѧ����ѧ�Ľ�ͨ��ʽ����У���꼶![]() ���4��ͬѧ���������һ�ݵ����ʾ����Ը�У����ѧ���������������
���4��ͬѧ���������һ�ݵ����ʾ����Ը�У����ѧ���������������![]() ��
��![]() �����г�
�����г�![]() ��
��![]() �˹�����
�˹�����![]() ��
��![]() ����
����![]() ��
��![]() ��˽�ҳ�
��˽�ҳ�![]() ��
��![]() ������ʽ
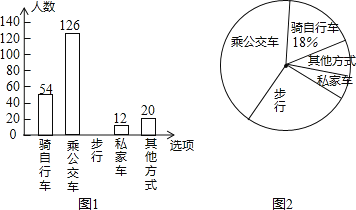
������ʽ![]() ����ѡ�Ҫ����ͬѧ���е�ѡ���������������Ƴ�����ͳ��ͼ1������ͳ��ͼ2������������Ϣ������������⣺
����ѡ�Ҫ����ͬѧ���е�ѡ���������������Ƴ�����ͳ��ͼ1������ͳ��ͼ2������������Ϣ������������⣺
![]() ���ν��ܵ������������______�ˣ���������ͳ��ͼ����������
���ν��ܵ������������______�ˣ���������ͳ��ͼ����������
![]() ������ͳ��ͼ�У�����˽�ҳ���������ռ�İٷֱ���______����������ʽ���������ε�Բ�ĽǶ�����______�ȣ�
������ͳ��ͼ�У�����˽�ҳ���������ռ�İٷֱ���______����������ʽ���������ε�Բ�ĽǶ�����______�ȣ�
![]() ��֪��4��ͬѧ����2��Ůͬѧ��Ҫ����ѡ����ͬѧ�㱨���������������б�������״ͼ�ķ��������ǡ��ѡ��1��������1��Ů���ĸ��ʣ�
��֪��4��ͬѧ����2��Ůͬѧ��Ҫ����ѡ����ͬѧ�㱨���������������б�������״ͼ�ķ��������ǡ��ѡ��1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
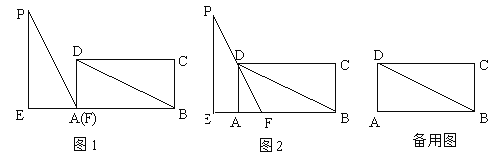
����Ŀ����ͼ1���ھ���ABCD�У�DB=6��AD=3����Rt��PEF�У���PEF=90�㣬EF=3��PF=6����PEF����F�͵�A�غϣ��ı�EF�;��εı�AB��ͬһֱ����.�ֽ�Rt��PEF��A��ÿ��1����λ���ٶ�������AB��������ƽ�ƣ�����F���B�غ�ʱֹͣ�˶������˶�ʱ��Ϊt�룬
����������⣺
��1����ͼ1������PD����գ���PFD= ���ı���PEAD������� ��
��2����ͼ2����PF������Dʱ���� ��PEF�˶�ʱ��t��ֵ��
��3�����˶��Ĺ����У�����PEF����ABD�ص��������ΪS�������S��t�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com