
【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是 分;选手乙的成绩的众数是 分;
(2)计算选手甲的平均成绩和方差;
(3)已知选手乙的成绩的方差是15,则成绩较稳定的是哪位选手?请直接写出结果.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
A | 60<x≤70 | 38 | 2 581 |
B | 70<x≤80 | 72 | 5 543 |
C | 80<x≤90 | 60 | 5 100 |
D | 90<x≤100 | m | 2 796 |

依据以上统计信息,解答下列问题:
(1)求得m=________,n=__________;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习与探究:
在等边△ABC中,P是射线AB上的一点.

(1)探索实践:
如图1,P是边AB的中点,D是线段CP上的一个动点,以CD为边向右侧作等边△CDE,DE与BC交于点M,连结BE.
①求证:AD=BE;
②连结BD,当DB+DM最小时,试在图2中确定D的位置,并说明理由;(要求用尺规作图,保留作图痕迹)
③在②的条件下,求△CME与△ACM的面积之比.
(2)思维拓展:
如图3,点P在边AB的延长线上,连接CP,点B关于直线CP的对称点为B',连结AB',CB',AB'交BC于点N,交直线CP于点G,连结BG.请判断∠AGC与∠AGB的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践﹣猜想、证明与拓广
问题情境:
数学课上同学们探究正方形边上的动点引发的有关问题,如图1,正方形ABCD中,点E是BC边上的一点,点D关于直线AE的对称点为点F,直线DF交AB于点H,直线FB与直线AE交于点G,连接DG,CG.
猜想证明
(1)当图1中的点E与点B重合时得到图2,此时点G也与点B重合,点H与点A重合.同学们发现线段GF与GD有确定的数量关系和位置关系,其结论为: ;
(2)希望小组的同学发现,图1中的点E在边BC上运动时,(1)中结论始终成立,为证明这两个结论,同学们展开了讨论:
小敏:根据轴对称的性质,很容易得到“GF与GD的数量关系”…
小丽:连接AF,图中出现新的等腰三角形,如△AFB,…
小凯:不妨设图中不断变化的角∠BAF的度数为n,并设法用n表示图中的一些角,可证明结论.
请你参考同学们的思路,完成证明;
(3)创新小组的同学在图1中,发现线段CG∥DF,请你说明理由;
联系拓广:
(4)如图3若将题中的“正方形ABCD”变为“菱形ABCD“,∠ABC=α,其余条件不变,请探究∠DFG的度数,并直接写出结果(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任丘市举办一场中学生乒乓球比赛,比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分费用与参加比赛的人数(x)人成正比.当x=20时,y=1600;当x=30时,y=2000.
(1)求y与x之间的函数关系式;
(2)如果承办此次比赛的组委会共筹集;经费6350元,那么这次比赛最多可邀请多少名运动员参赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
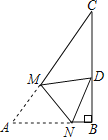
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).

(1)写出点C及点C关于y轴对称的点C′的坐标;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
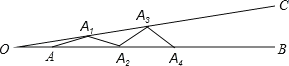
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
A. 10B. 9C. 8D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com