
【题目】学习与探究:
在等边△ABC中,P是射线AB上的一点.

(1)探索实践:
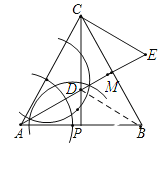
如图1,P是边AB的中点,D是线段CP上的一个动点,以CD为边向右侧作等边△CDE,DE与BC交于点M,连结BE.
①求证:AD=BE;
②连结BD,当DB+DM最小时,试在图2中确定D的位置,并说明理由;(要求用尺规作图,保留作图痕迹)
③在②的条件下,求△CME与△ACM的面积之比.
(2)思维拓展:
如图3,点P在边AB的延长线上,连接CP,点B关于直线CP的对称点为B',连结AB',CB',AB'交BC于点N,交直线CP于点G,连结BG.请判断∠AGC与∠AGB的大小关系,并证明你的结论.
【答案】(1)①见解析,②见解析,③1:3;(2)∠AGC=∠AGB,理由见解析
【解析】
1)探索实践
①根据等边三角形的性质可得AC=BC,CD=CE,∠ACB=∠DCE=60°,可得∠ACD=∠BCE,根据“SAS”可证△ACD≌△BCE,即可得AD=BE;
②根据等腰三角形的性质可得AD=BD,即BD+DM=AD+DM,则当点A,点D,点M三点共线且AM⊥BC时,BD+DM值最小,即AM平分∠CAB;
③根据等边三角形的性质可求AM=3ME,由△CME与△ACM是等高的两个三角形,即△CME与△ACM的面积之比等于ME与AM的比值;
(2)思维拓展
根据轴对称的性质和等腰三角形的性质可得∠CAB'=∠CBG,可证点A,点B,点G,点C四点共圆,可得∠AGC=∠ABC=60°,∠AGB=∠ACB=60°,即∠AGC=∠AGB.
(1)探索实践
①在等边△ABC与等边△CDE中:AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠ACD+∠DCM=∠DCM+∠BCE,
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
∴AD=BE
(2)②如图,作∠BAC的平分线交CP于D,连结BD,
∵P是边等边△ABC中AB边的中点
∴CP是AB边上的中线,
由“等腰三角形的三线合一”性质知,CP是AB的垂直平分线,CP平分∠ACB,
∴DB=DA,∠PCB=30°
要使DB+DM最小,只要DA+DM最小,即当A,D,M共线时,且AM⊥BC时,AM最小,
此时DB+DM最小
③∵∠ACD=∠CAD=∠DCM=∠ECM=30°,CM⊥AM
∴DC=DA=DE,DM=EM=![]() DE,
DE,
∴AM=3ME
又∵Rt△CME的边ME上的高与Rt△ACM的边AM上的高均是CM
∴S△CME:S△ACM=1:3
(2)思维拓展
∠AGC=∠AGB
理由如下:∵点B关于直线CP的对称点为B',
∴BC=CB',∠CB'G=∠CBG,
∴AC=BC=B'C
∴∠CAB'=∠CB'A,
∴∠CAB'=∠CBG,
∴点A,点B,点G,点C四点共圆,
∴∠AGC=∠ABC=60°,∠AGB=∠ACB=60°,
∴∠AGC=∠AGB


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是( )
![]() 弧AB的度数等于弧CD的度数;
弧AB的度数等于弧CD的度数;![]() 所对的圆心角等于弧CD所对的圆心角;
所对的圆心角等于弧CD所对的圆心角;
![]() 弧AB和弧CD是等弧;
弧AB和弧CD是等弧;![]() 弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.
弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:
①玩家只能将小兔从A、B两个出入口放入;
②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元.
(1)问小美得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为_____m(结果保留一位小数,参考数据:sin53°≈![]() , cos53°≈
, cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD垂直平分线段AB,垂足为H,CA的延长线交BD的延长线于E,CB的延长线交AD的延长线于F.

(1)求证:DE=DF;
(2)若AE=AB,∠E=22.5°,则直接写出图中内角含有45°等腰三角形(写出3个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:材料1:如果一个多项式中的字母按照任何次序轮换后,原多项式不变,那么称该多项式是轮换多项式,简称轮换式.例如:多项式![]() ,将字母
,将字母![]() 换字母
换字母![]() ,字母
,字母![]() 换字母
换字母![]() ,得到多项式
,得到多项式![]() ,而
,而![]() ,所以多项式
,所以多项式![]() 是轮换式.我们把含有两个字母的轮换式称为二元轮换式,其中含字母
是轮换式.我们把含有两个字母的轮换式称为二元轮换式,其中含字母![]() ,
,![]() 的二元轮换式的基本轮换式是
的二元轮换式的基本轮换式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等二元轮换式都可以用
等二元轮换式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
材料2:因为![]() ,所以,对于二次项系数为1的二次三项式
,所以,对于二次项系数为1的二次三项式![]() 的因式分解,就是把常数项
的因式分解,就是把常数项![]() 分解成两个数的积,且使这两数的和等于
分解成两个数的积,且使这两数的和等于![]() ,即如果有
,即如果有![]() ,
,![]() 两数满足
两数满足![]() ,
,![]() ,则有
,则有![]() .如分解因式
.如分解因式![]() :因为
:因为![]() ,
,![]() ,所以
,所以![]() .
.
请根据以上材料解决下列问题:
(1)式子①![]() ;②
;②![]() ;③
;③![]() ,④
,④![]() 中,属于轮换式的是 (填序号);
中,属于轮换式的是 (填序号);
(2)因式分解:![]() ;
;![]() ;
;
(3)若![]() (其中
(其中![]() ),且
),且![]() ,求
,求![]() 的值并把式子
的值并把式子![]() 因式分解.
因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是 分;选手乙的成绩的众数是 分;
(2)计算选手甲的平均成绩和方差;
(3)已知选手乙的成绩的方差是15,则成绩较稳定的是哪位选手?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com