
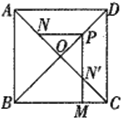
【题目】如图,在正方形ABCD中,AB=4,AC与![]() 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交
相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交![]() 于点N′,则PN-MN′的值为( )
于点N′,则PN-MN′的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据正方形的性质可得点O为AC的中点,根据三角形中位线的性质可求出PN的长,由PM⊥BC可得PM//CD,根据点P为OD中点可得点N′为OC中点,即可得出AC=4CN′,根据MN′//AB可得△CMN′∽△CBA,根据相似三角形的性质可求出MN′的长,进而可求出PN-MN′的长.
∵四边形ABCD是正方形,AB=4,
∴OA=OC,AD=AB=4,
∵N是AO的中点,P是OD的中点,
∴PN是△AOD的中位线,
∴PN=![]() AD=2,
AD=2,
∵PM⊥BC,
∴PM//CD//AB,
∴点N′为OC的中点,
∴AC=4CN′,
∵PM//AB,
∴△CMN′∽△CBA,
∴![]()
![]() ,
,
∴MN′=1,
∴PN-MN′=2-1=1,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
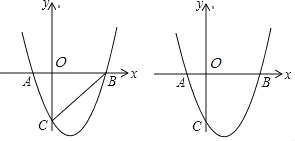
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
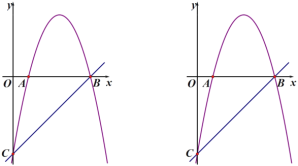
(1)求抛物线的函数表达式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一动点,求
上方抛物线上的一动点,求![]() 面积
面积![]() 的最大值并求出此时点
的最大值并求出此时点![]() 的坐标;
的坐标;
(3)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的一个夹角等于
的一个夹角等于![]() 的3倍时,请直接写出点
的3倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果![]() (千克),增种果树
(千克),增种果树![]() (棵), 它们之间的函数关系如图所示.
(棵), 它们之间的函数关系如图所示.
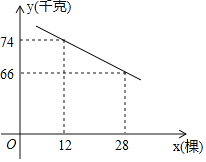
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上![]() 处垂直于地面竖立了高度为
处垂直于地面竖立了高度为![]() 米的标杆
米的标杆![]() ,这时地面上的点
,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上,测得
正好在同一直线上,测得![]() 米,将标杆向后平移到点
米,将标杆向后平移到点![]() 处,这时地面上的点
处,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上(点
正好在同一直线上(点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 与古塔底处的点
与古塔底处的点![]() 在同一直线上) ,这时测得
在同一直线上) ,这时测得![]() 米,
米,![]() 米,请你根据以上数据,计算古塔的高度
米,请你根据以上数据,计算古塔的高度![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
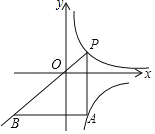
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
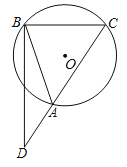
【题目】如图,⊙O的半径为2,弦AB的长为2![]() ,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,弦AB=![]() ,BC=
,BC=![]() ,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.
,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.
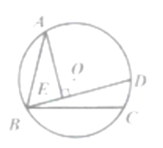
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com