
【题目】如图,矩形ABCD的边AD是菱形AEDF的一条对角线,且点E在矩形ABCD的边BC上.
(1)求证:△ABE≌△DCE;
(2)直接写出当矩形边长AD与AB之间满足什么关系时,菱形AEDF为正方形.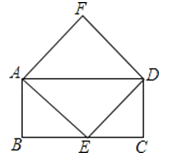
【答案】(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,AD=BC,
∵四边形AEDF是菱形,
∴AE=DE,
在Rt△ABE和Rt△DCE中,![]() ,
,
∴Rt△ABE≌Rt△DCE(HL);
(2)解:当AD=2AB时,菱形AEDF为正方形;理由如下:
∵Rt△ABE≌Rt△DCE,
∴BE=CE,∠AEB=∠DEC,
∵AD=2AB,AD=BC,
∴AB=BE,
∴△ABE是等腰直角三角形,
∴∠AEB=45°,
∴∠DEC=45°,
∴∠AED=180°﹣45°﹣45°=90°,
∴菱形AEDF为正方形.
【解析】(1)由矩形的性质得出AB=DC,∠B=∠C=90°,由菱形的性质得出AE=DE,由HL证明Rt△ABE≌Rt△DCE即可;
(2)由全等三角形的性质得出BE=CE,∠AEB=∠DEC,由AD=2AB,证出△ABE是等腰直角三角形,得出∠AEB=45°,证出∠AED=90°,即可得出菱形AEDF为正方形.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).


科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计算;月用水量超过20
计算;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 计算,超过部分按2.6元/
计算,超过部分按2.6元/![]() 计算. 设某户家庭月用水量
计算. 设某户家庭月用水量![]()
![]() .
.

(1)用含![]() 的式子表示:
的式子表示:
当0≤![]() ≤20时,水费为 元;
≤20时,水费为 元;
当![]() >20时,水费为 元.
>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】悦达汽车4S店“十一”黄金周销售某种型号汽车,该型号汽车的进价为30万元/辆,若黄金周期间销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,黄金周期间销售量不会突破30台.已知该型号汽车的销售价为32万元/辆,悦达汽车4S店计划黄金周期间销售利润25万元,那么需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=![]() CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为
CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为 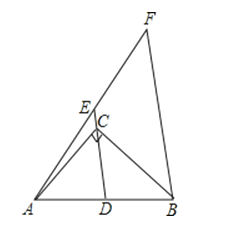
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com