
【题目】已知点A(a,0)、B(b,0),且 ![]() +|b﹣2|=0.
+|b﹣2|=0. 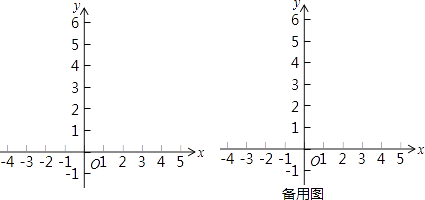
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的 ![]() ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】
(1)解:∵(a+4)2+|b﹣2|=0,
∴a+4=0,b﹣2=0,
∴a=﹣4,b=2
(2)解:如图1,
∵A(﹣4,0)、B(2,0),
∴AB=6,
∵三角形ABC的面积是15,
∴ ![]() ABOC=15,
ABOC=15,
∴OC=5,
∴C(0,5)

(3)解:存在,如图2,
∵三角形ABC的面积是15,
∴S△ACD= ![]() CDOC=15,
CDOC=15,
∴ ![]() CD×5=
CD×5= ![]() ×15,
×15,
∴CD=3,
∴D(3,5)或(﹣3,5).

【解析】(1)根据非负数的性质列方程即可得到结论;(2)由A(﹣4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15列方程即可得到即可;(3)根据三角形ABC的面积是15列方程即可得到结论.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】计算.
(1)a24÷[(a2) 3) 4;
(2)( a3·a4) 2÷(a3) 2÷a;
(3)- x12÷(-x4) 3;
(4)( x6÷x4·x2) 2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 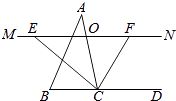
(1)求证:EO=FO;
(2)当CE=12,CF=10时,求CO的长;
(3)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P是线段AB的黄金分割点,且AP>PB,则有( )
A. AB2=APPB B. AP2=BPAB
C. BP2=APAB D. APAB=PBAP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F. 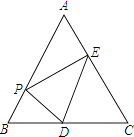
(1)求∠APE的度数;
(2)连接DE,当△PDE为等边三角形时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,哪些适合抽样调查?哪些适合全面调查?
(1)工厂准备对一批即将出厂的饮料中含有细菌总数的情况进行调查;
(2)小明准备对全班同学所喜爱的球类运动的情况进行调查;
(3)某农田保护区对区内的水稻秧苗的高度进行调查.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com