
 如图,某军港有一雷达站,军舰停泊在雷达站的南偏东60°方向36海里处,另一艘军舰位于军舰的正西方向,与雷达站相距18
如图,某军港有一雷达站,军舰停泊在雷达站的南偏东60°方向36海里处,另一艘军舰位于军舰的正西方向,与雷达站相距18| 2 |
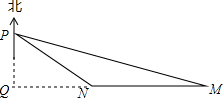 解:过点P作PQ⊥MN,交MN的延长线于点Q.
解:过点P作PQ⊥MN,交MN的延长线于点Q.| 1 |
| 2 |
| 1 |
| 2 |
| PQ |
| PN |
| 18 | ||
18
|
| ||
| 2 |
| 3 |
| 3 |
| 3 |


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
| a |
| b |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在某一电路中,电源电压U保持不变,电流I,电压U,电阻R三者之间满足关系I=
在某一电路中,电源电压U保持不变,电流I,电压U,电阻R三者之间满足关系I=| U |
| R |
查看答案和解析>>
科目:初中数学 来源: 题型:
 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.
光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com