
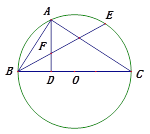
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.
【答案】(1)∠ACB=∠BAD,理由见解析;(2)△FAB是等腰三角形
【解析】试题分析:(1)根据圆周角定理求出∠BAC=90°,根据三角形内角和定理和垂直求出∠ACB+∠ABC=90°,∠BAD+∠ABC=90°,即可得出答案;(2)根据圆周角定理求出∠ACB=∠ABE,推出∠BAD=∠ABE,根据等腰三角形的判定得出即可.
试题解析:(1)因为BC是⊙O的直径,
所以∠CAB=90°,
所以∠ABD+∠ACB=90°,
因为AD⊥BC,
所以∠ABD+∠BAD=90°,
所以∠ACB=∠BAD;
(2)△FAB是等腰三角形。
因为![]() ,
,
所以∠ACB=∠BAD,
又∠ACB=∠BAD,
所以∠BAD=∠ABF,
所以△FAB是等腰三角形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答问题:
如图,
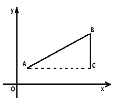
点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是![]() ,
,![]() ,所以
,所以![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.
的值看作点(x1,y1)到点(x2,y2)的距离.
例如:![]()
![]()
![]()
![]()
故代数式![]() 的值看作点(x,y)到点(1,-1)的距离.
的值看作点(x,y)到点(1,-1)的距离.
已知:代数式![]()
(1)该代数式的值可看作点(x,y)到点 、 的距离之和.
(2)求出这个代数式的最小值,
(3)在(2)的条件下求出此时y与x之间的函数关系式并写出x的值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学海书店购一批故事书进行销售,其进价为每本40元,如果按每本故事书50元进行出售,每月可以售出500本故事书,后来经过市场调查发现,若每本故事书涨价1元,则故事书的销量每月减少20本.
(1)若学海书店要保证每月销售此种故事书盈利6000元,同时又要使购书者得到实惠,则每本故事书需涨价多少元;
(2)若使该故事书的月销量不低于300本,则每本故事书的售价应不高于多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(x1,y1)和(x2,y2)都在函数y=﹣2x+4的图象上.则下列结论正确的是( )
A. 若y1<y2,则x1<x2B. 若y1﹣y2=2,则x1﹣x2=﹣1
C. 可由直线y=2x向上平移4个单位得到D. 与坐标系围成的三角形面积为8
查看答案和解析>>
科目:初中数学 来源: 题型:
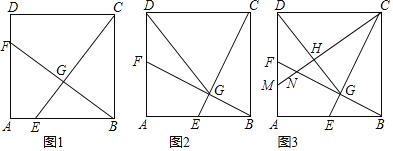
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,当点![]() 运动到
运动到![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,分别交
,分别交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com