
【题目】阅读下列材料,回答问题:
如图,
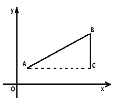
点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是![]() ,
,![]() ,所以
,所以![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.
的值看作点(x1,y1)到点(x2,y2)的距离.
例如:![]()
![]()
![]()
![]()
故代数式![]() 的值看作点(x,y)到点(1,-1)的距离.
的值看作点(x,y)到点(1,-1)的距离.
已知:代数式![]()
(1)该代数式的值可看作点(x,y)到点 、 的距离之和.
(2)求出这个代数式的最小值,
(3)在(2)的条件下求出此时y与x之间的函数关系式并写出x的值范围.
【答案】(1)(1,-8), (-2,2); (2)![]() ;(3)
;(3)![]()
【解析】
(1)利用配方法将代数式中的被开方数配成完全平方式,再根据题中给出的两点之间距离的定义即可求出结果.
(2)画出图形观察即可发现当点(x,y)与点(1,-8),(-2,2)在同一条直线上,并且点(x,y)位于点(1,-8),(-2,2)的之间时,代数式的值最小;
(3)利用待定系数法,列出二元一次方程组解出未知数的值即可.
解:(1)根据材料知:
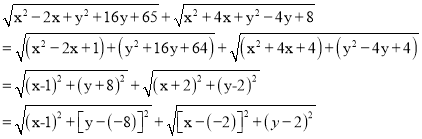
所以可将代数式![]() 的值看作点(x,y)到点(1,-8)的距离与点(x,y)到点(-2,2)的距离之和.
的值看作点(x,y)到点(1,-8)的距离与点(x,y)到点(-2,2)的距离之和.
(2)当代数式![]() 取最小值时,即点(x,y)与点(1,-8),(-2,2)在同一条直线上,并且点(x,y)位于点(1,-8),(-2,2)的中间,
取最小值时,即点(x,y)与点(1,-8),(-2,2)在同一条直线上,并且点(x,y)位于点(1,-8),(-2,2)的中间,
∴![]() 的最小值
的最小值![]()
(3)设过(x,y),且-2≤x≤1,(1,-8),(-2,2)的直线解析式为:y=kx+b则
![]() 解得:
解得: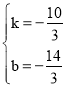
∴![]()


科目:初中数学 来源: 题型:
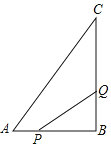
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A出发,沿AB边向点B以1cm/s的速度移动;点Q从点B出发,沿BC边向点C以2cm/s的速度移动,设P,Q同时出发,问:
(1)经过几秒后,点P,Q之间距离最小?最小距离是多少?
(2)经过几秒后,△PBQ的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决材料后的问题:
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为:f(x)=![]() ,例如17与16的友好数为f(17,16)=
,例如17与16的友好数为f(17,16)=![]() =
=![]() .
.
材料二:对于实数x,用[x]表示不超过实数x的最大整数,即满足条件[x]≤x<[x]+1,例如:
[﹣1.5]=[﹣1.6]=﹣2,[0]=[0.7]=0,[2.2]=[2.7]=2,……
(1)由材料一知:x2+2与1的“友好数”可以用f(x2+2,1)表示,已知f(x2+2,1)=2,请求出x的值;
(2)已知[![]() a﹣1]=﹣3,请求出实数a的取值范围;
a﹣1]=﹣3,请求出实数a的取值范围;
(3)已知实数x、m满足条件x﹣2[x]=![]() ,且m≥2x+
,且m≥2x+![]() ,请求f(x,m2﹣
,请求f(x,m2﹣![]() m)的最小值.
m)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
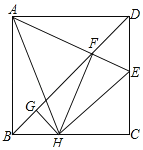
【题目】如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于F,过F作FH⊥AE交BC于点H,过H作HG⊥BD于G,连结AH.在以下四个结论中:①AF=HE;②∠HAE=45°;③FC=2![]() ;④△CEH的周长为12.其中正确的结论有_____.
;④△CEH的周长为12.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() ,给出下列说法:①若
,给出下列说法:①若![]() ,则方程必有两个实数根;②若
,则方程必有两个实数根;②若![]() ,则方程必有两个实数根;③若
,则方程必有两个实数根;③若![]() ,则方程有两个不相等的实数根;④若
,则方程有两个不相等的实数根;④若![]() ,则方程一定没有实数根.其中说法正确的序号是( )
,则方程一定没有实数根.其中说法正确的序号是( )
A. ①②③B. ①②④
C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
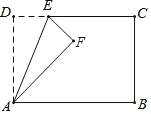
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点M,与y轴交于点A,过点A作
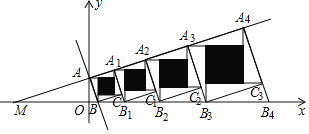
与x轴交于点M,与y轴交于点A,过点A作![]() ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,
,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,![]() 中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
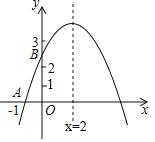
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:①abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() ;⑤c-3a>0其中正确结论有( )
;⑤c-3a>0其中正确结论有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
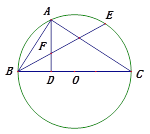
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com