
【题目】阅读下列材料,解决材料后的问题:
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为:f(x)=![]() ,例如17与16的友好数为f(17,16)=
,例如17与16的友好数为f(17,16)=![]() =
=![]() .
.
材料二:对于实数x,用[x]表示不超过实数x的最大整数,即满足条件[x]≤x<[x]+1,例如:
[﹣1.5]=[﹣1.6]=﹣2,[0]=[0.7]=0,[2.2]=[2.7]=2,……
(1)由材料一知:x2+2与1的“友好数”可以用f(x2+2,1)表示,已知f(x2+2,1)=2,请求出x的值;
(2)已知[![]() a﹣1]=﹣3,请求出实数a的取值范围;
a﹣1]=﹣3,请求出实数a的取值范围;
(3)已知实数x、m满足条件x﹣2[x]=![]() ,且m≥2x+
,且m≥2x+![]() ,请求f(x,m2﹣
,请求f(x,m2﹣![]() m)的最小值.
m)的最小值.
【答案】(1)x=±2;(2)﹣4≤a<﹣2;(3)当m=![]() 时,y有最大值是﹣
时,y有最大值是﹣![]() ,此时f(x,m2﹣
,此时f(x,m2﹣![]() m)有最小值,最小值是﹣
m)有最小值,最小值是﹣![]() .
.
【解析】
(1)由题意得到![]() ,计算即可得到答案;
,计算即可得到答案;
(2)由题意得到![]() ,解不等式即可得到答案;
,解不等式即可得到答案;
(3)先由题意得到![]() ,则
,则![]() ,设
,设![]() ,由题意得到
,由题意得到![]() ,设y=﹣2m2+3m﹣4,根据二次函数的性质即可得到答案.
,设y=﹣2m2+3m﹣4,根据二次函数的性质即可得到答案.
解:(1)∵f(x2+2,1)=2,
∴![]() ,
,
∴x2=4,
∴x=±2;
(2)∵[x]≤x<[x]+1,
∴![]() ,
,
解得﹣4≤a<﹣2;
(3)∵x﹣2[x]=![]() ,
,
∴[x]=![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
又x=2k+![]() ,
,
∴![]() ,
,
∴整数k=﹣3,
∴x=![]() ,
,
又![]() ,
,
∴f(x,m2﹣![]() m),
m),
= ,
,
= ,
,
=![]() ,
,
设y=﹣2m2+3m﹣4,
则y=﹣2(m![]() )2
)2![]() ,
,
∵﹣2<0,
∴当m=![]() 时,y有最大值是
时,y有最大值是![]() ,此时f(x,m2﹣
,此时f(x,m2﹣![]() m)有最小值,最小值是
m)有最小值,最小值是![]() =﹣
=﹣![]() ,
,
此时最小值为﹣![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作试验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
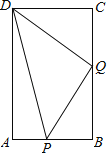
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.问:
(1)几秒时△PBQ的面积等于8cm2;
(2)几秒时△PDQ的面积等于28cm2;
(3)几秒时PQ⊥DQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
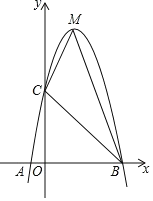
(1)求抛物线的解析式;
(2)求△MCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() 的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30
的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30![]() ,则点C的坐标为( )
,则点C的坐标为( )

A. ![]() B.
B.  C.
C. 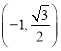 D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于A.B两点,且A点坐标为(3,0),经过B点的直线y=x-1交抛物线于点D.
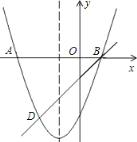
(1)求B点坐标和抛物线的解析式
(2)点D的坐标
(3)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答问题:
如图,
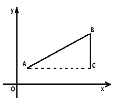
点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是![]() ,
,![]() ,所以
,所以![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.
的值看作点(x1,y1)到点(x2,y2)的距离.
例如:![]()
![]()
![]()
![]()
故代数式![]() 的值看作点(x,y)到点(1,-1)的距离.
的值看作点(x,y)到点(1,-1)的距离.
已知:代数式![]()
(1)该代数式的值可看作点(x,y)到点 、 的距离之和.
(2)求出这个代数式的最小值,
(3)在(2)的条件下求出此时y与x之间的函数关系式并写出x的值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com