练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小林准备进行如下操作试验：把一根长为的铁丝剪成两段，并把每一段各围成一个正方形．

    （1）要使这两个正方形的面积之和等于，小林该怎么剪？

    （2）小峰对小林说：“这两个正方形的面积之和不可能等于．”他的说法对吗？请说明理由．

    【答案】（1）小林应把铁丝剪成和的两段；（2）对.

    【解析】

    （1）设其中一个正方形的边长为，则另一个正方形的边长为，根据正方形的面积公式即可列出方程进行求解；

    （2）根据题意列出方程，对根进行判别即可求解.

    解：（1）设其中一个正方形的边长为，

    则另一个正方形的边长为．

    由题意，得．

    解得，．

    ，．

    所以小林应把铁丝剪成和的两段．

    （2）对，理由如下：

    假设能围成．由（1），得．

    化简，得．

    因为，

    所以此方强没有实数根．

    所以小峰的说法是对的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

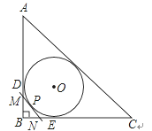
    【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧DE（不包括端点D，E）上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为4cm，则Rt△MBN的周长为________cm.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

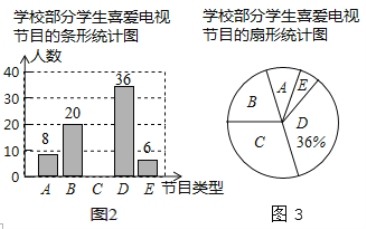
    【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调査（问卷调査表如图1所示），并根据调查结果绘制了图2、图3两幅统计图（均不完整），请根据统计图解答下列问题．

    （1）本次接受问卷调查的学生有________名．

    （2）补全条形统计图．

    （3）扇形统计图中B类节目对应扇形的圆心角的度数为________．

    （4）该校共有2000名学生，根据调查结果估计该校最喜爱新闻节目的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC，BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点，连接EM，MF，FN，NE，要使四边形EMFN为正方形，则需添加的条件是( )

    A. AB＝CD，AB⊥CDB. AB＝CD，AD＝BC

    C. AB＝CD，AC⊥BDD. AB＝CD，AD∥BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（　　）

    A. 当AB=BC时，四边形ABCD是菱形

    B. 当AC⊥BD时，四边形ABCD是菱形

    C. 当∠ABC=90°时，四边形ABCD是矩形

    D. 当AC=BD时，四边形ABCD是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

    （1）求证：四边形AMDN是平行四边形；

    （2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

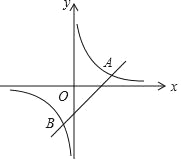
    【题目】如图，已知一次函数y=x﹣2与反比例函数y=的图象交于A、B两点．

    （1）求A、B两点的坐标；

    （2）观察图象，直接写出一次函数值小于反比例函数值的x的取值范围；

    （3）坐标原点为O，求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

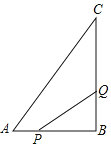
    【题目】如图，在△ABC中，∠B=90°，AB=6cm，BC=12cm.点P从点A出发，沿AB边向点B以1cm/s的速度移动；点Q从点B出发，沿BC边向点C以2cm/s的速度移动，设P，Q同时出发，问：

    (1)经过几秒后，点P，Q之间距离最小？最小距离是多少？

    (2)经过几秒后，△PBQ的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，解决材料后的问题：

    材料一：对于实数x、y，我们将x与y的“友好数”用f（x，y）表示，定义为：f（x）＝，例如17与16的友好数为f（17，16）＝＝．

    材料二：对于实数x，用[x]表示不超过实数x的最大整数，即满足条件[x]≤x＜[x]+1，例如：

    [﹣1.5]＝[﹣1.6]＝﹣2，[0]＝[0.7]＝0，[2.2]＝[2.7]＝2，……

    （1）由材料一知：x2+2与1的“友好数”可以用f（x2+2，1）表示，已知f（x2+2，1）＝2，请求出x的值；

    （2）已知[a﹣1]＝﹣3，请求出实数a的取值范围；

    （3）已知实数x、m满足条件x﹣2[x]＝，且m≥2x+，请求f（x，m2﹣m）的最小值．

    查看答案和解析>>

    同步练习册答案