
【题目】如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于F,过F作FH⊥AE交BC于点H,过H作HG⊥BD于G,连结AH.在以下四个结论中:①AF=HE;②∠HAE=45°;③FC=2![]() ;④△CEH的周长为12.其中正确的结论有_____.
;④△CEH的周长为12.其中正确的结论有_____.
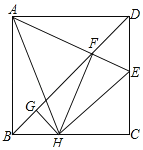
【答案】②④.
【解析】
①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
②由FH⊥AE,AF=FH,可得:∠HAE=45°;
③F是动点,CF的长度不是定值;
④作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CE=IM,故△CEH的周长为边AM的长,为定值.
解:①连接FC,延长HF交AD于点L,
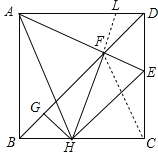
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF.故①错误,
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③∵F是动点,CF的长度不是定值,本选项错误;
④延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,
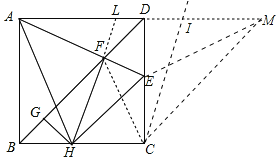
根据△MEC≌△CIM,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=12.
∴△CEH的周长为12,为定值.
故②④结论都正确.
故答案为②④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
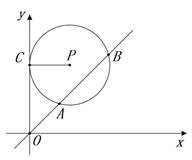
【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() 的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30
的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B.C在函数图象上,四边形OBAC为菱形,且∠AOB=30![]() ,则点C的坐标为( )
,则点C的坐标为( )

A. ![]() B.
B.  C.
C. 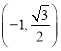 D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于A.B两点,且A点坐标为(3,0),经过B点的直线y=x-1交抛物线于点D.
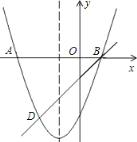
(1)求B点坐标和抛物线的解析式
(2)点D的坐标
(3)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与反比例函数y=![]() (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.

(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=![]() (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.
①当t=![]() 时,求线段EF的长;
时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答问题:
如图,
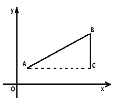
点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1),于是![]() ,
,![]() ,所以
,所以![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.
的值看作点(x1,y1)到点(x2,y2)的距离.
例如:![]()
![]()
![]()
![]()
故代数式![]() 的值看作点(x,y)到点(1,-1)的距离.
的值看作点(x,y)到点(1,-1)的距离.
已知:代数式![]()
(1)该代数式的值可看作点(x,y)到点 、 的距离之和.
(2)求出这个代数式的最小值,
(3)在(2)的条件下求出此时y与x之间的函数关系式并写出x的值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作![]() 交AB于点F,连接DB交
交AB于点F,连接DB交![]() 于点H,E是BC上的一点,且
于点H,E是BC上的一点,且![]() ,连接DE.
,连接DE.

(1)求证:DE是![]() 的切线.
的切线.
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com