
【题目】如图,四边形ABCD为菱形,以AD为直径作![]() 交AB于点F,连接DB交
交AB于点F,连接DB交![]() 于点H,E是BC上的一点,且
于点H,E是BC上的一点,且![]() ,连接DE.
,连接DE.

(1)求证:DE是![]() 的切线.
的切线.
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)![]() 的半径为
的半径为![]() .
.
【解析】
(1)如图1,连接DF,先根据菱形的性质和SAS证明△DAF≌△DCE,得![]() ,再由AD是圆的直径得∠AFD=90°,于是∠DEC=90°,然后利用
,再由AD是圆的直径得∠AFD=90°,于是∠DEC=90°,然后利用![]() 可得∠ADE=90°,问题即得证明;
可得∠ADE=90°,问题即得证明;
(2)如图2,连接AH,先根据等腰三角形三线合一的性质得出![]() ,再由DF是
,再由DF是![]() 和
和![]() 的公共的直角边,根据勾股定理列出关于AD的方程,解方程即可求出AD的长,进一步即可求出圆的半径.
的公共的直角边,根据勾股定理列出关于AD的方程,解方程即可求出AD的长,进一步即可求出圆的半径.
(1)证明:如图1,连接DF,
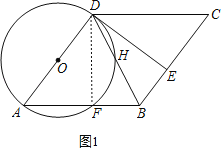
∵四边形ABCD为菱形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() .
.
∵AD是![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵OD是![]() 的半径,∴DE是
的半径,∴DE是![]() 的切线;
的切线;
(2)解:如图2,连接AH,
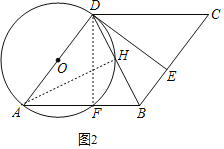
∵AD是![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的半径为
的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于F,过F作FH⊥AE交BC于点H,过H作HG⊥BD于G,连结AH.在以下四个结论中:①AF=HE;②∠HAE=45°;③FC=2![]() ;④△CEH的周长为12.其中正确的结论有_____.
;④△CEH的周长为12.其中正确的结论有_____.
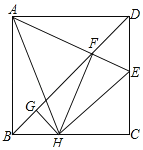
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
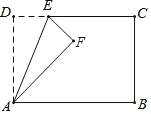
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点M,与y轴交于点A,过点A作
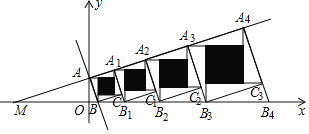
与x轴交于点M,与y轴交于点A,过点A作![]() ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,
,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,![]() 中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
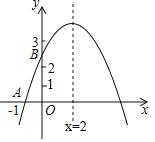
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:①abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() ;⑤c-3a>0其中正确结论有( )
;⑤c-3a>0其中正确结论有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作试验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com