
【题目】已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD=_____.
科目:初中数学 来源: 题型:
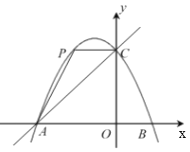
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
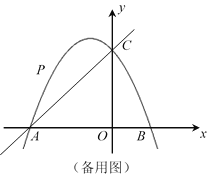
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
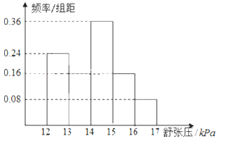
【题目】为了研究某药品的疗效,现选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组、第二组、…、第五组.如图是根据试验数据制成的频率分布直方图.
(1)若第一组接受治疗的志愿者有12人,则第三组接受治疗的志愿者有多少人?
(2)若接受治疗的志愿者共有50人,规定舒张压在14kpa以上的志愿者接受进一步的临床试验,若从三组志愿者中按比例分配20张床位,则舒张压数据在[14,15)的志愿者总共可以得到多少张床位?
查看答案和解析>>
科目:初中数学 来源: 题型:
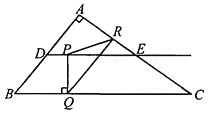
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,女生楼在男生楼墙面上的影高为DA.已知CD=42m.求楼间距AB的长度为多少米?(参考数据:sin32.3°=0.53,cos32.3°=0.85,tan32.3°=0.63,sin55.7°=0.83,cos55.7°=0.56,tan55.7°=1.47)
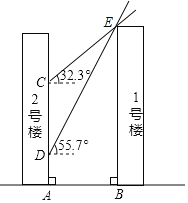
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=6,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
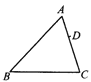
A.8B.![]() C.8或
C.8或![]() D.8或9
D.8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
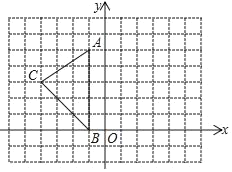
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3)
(1)将△ABC向右平移6个单位至△A1B1C1,再将△A1B1C1绕点E(5,1)逆时针旋转90°至△A2B2C2,请按要求画出图形;
(2)在(1)的变换过程中,直接写出点C的运动路径长
(3)△A2B2C2可看成△ABC绕某点P旋转90°得到的,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
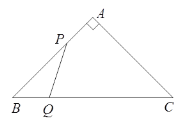
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com