
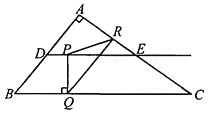
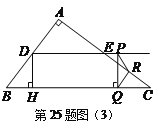
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由
【答案】(1)![]() ;
;
(2)![]() .
.
(3)当![]() 为
为![]() 或6或
或6或![]() 时,△PQR为等腰三角形.
时,△PQR为等腰三角形.
【解析】
(1)根据△RQC∽△ABC,根据相似三角形的对应边成比例可求解DH;
(2)根据三角形的相似比求出y关于x的函数关系式;
(3)画出图形,根据图形进行讨论:
① 当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,∴∠1=∠C.
∴cos∠1=cosC=![]() =
=![]() ,∴
,∴![]() ,即可求出x的值;
,即可求出x的值;
② 当PQ=RQ时,-![]() x+6=
x+6=![]() ,x=6;
,x=6;
③当PR=QR时,则R为PQ中垂线上的点,于是点R为EC的中点,故CR=![]() CE=
CE=![]() AC=2.
AC=2.
(1)![]() ,AB=6,AC=8,
,AB=6,AC=8,![]() .
.
![]() 点D为AB中点,
点D为AB中点,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
∴![]() ,
,
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() 关于
关于![]() 的函数关系式为:
的函数关系式为:![]() .
.
(3)存在,分三种情况:
①如图(1),当![]() 时,过点P作
时,过点P作![]() 于M,则
于M,则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
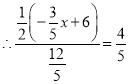 ,
,
![]() .
.
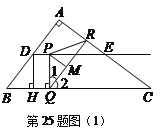
②如图(2),当![]() 时,
时,
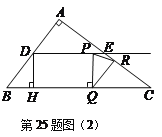
![]() ,
,
![]() .
.
③如图(3),当![]() 时,则R为PQ中垂线上的点,于是点R为EC的中点,
时,则R为PQ中垂线上的点,于是点R为EC的中点,
![]() .
.
![]() ,
,
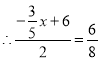 ,
,
![]() .
.
综上所述,当![]() 为
为![]() 或6或
或6或![]() 时,△PQR为等腰三角形.
时,△PQR为等腰三角形.


科目:初中数学 来源: 题型:
【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
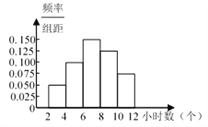
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
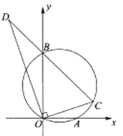
A. ①②B. ②③C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
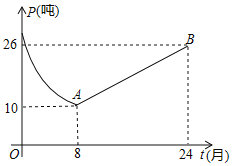
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数p=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:
Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为W(单位:万元).
①求W关于t的函数解析式;
②第几个月销售该原料药的月毛利润最大?对应的月销售量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
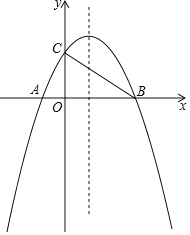
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点D为抛物线对称轴上一点,连接CD、BD,若∠DCB=∠CBD,求点D的坐标;
(3)已知F(1,1),若E(x,y)是抛物线上一个动点(其中1<x<2),连接CE、CF、EF,求△CEF面积的最大值及此时点E的坐标.
(4)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 型两种客车,它们的载客量和租金如下表:
型两种客车,它们的载客量和租金如下表:
|
| |
载客量/(人/辆) |
|
|
租金/(元/辆) |
|
|
某学校计划在总费用![]() 元的限额内,租用
元的限额内,租用![]() 、
、![]() 型客车共5辆送九年级师生集体外出活动.
型客车共5辆送九年级师生集体外出活动.
(Ⅰ)设租用![]() 型客车
型客车![]() 辆(
辆(![]() 为非负整数),根据题意,用含
为非负整数),根据题意,用含![]() 的式子填写下表:
的式子填写下表:
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
(Ⅱ)若九年级师生共有![]() 人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com