
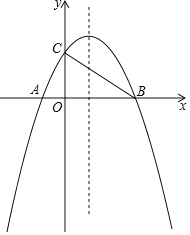
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求该抛物线的解析式,并写出它的对称轴;
(2)点D为抛物线对称轴上一点,连接CD、BD,若∠DCB=∠CBD,求点D的坐标;
(3)已知F(1,1),若E(x,y)是抛物线上一个动点(其中1<x<2),连接CE、CF、EF,求△CEF面积的最大值及此时点E的坐标.
(4)若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+2;∴对称轴x=1;(2)D(1,
x+2;∴对称轴x=1;(2)D(1,![]() );(3)最大值是
);(3)最大值是![]() ,此时E(
,此时E(![]() ,
,![]() );(4)M(2,2)或M(4,-
);(4)M(2,2)或M(4,-![]() )或M(-2,-
)或M(-2,-![]() ).
).
【解析】
(1)将点A(-1,0),B(3,0)代入y=ax2+bx+2即可;
(2)过点D作DG⊥y轴于G,作DH⊥x轴于H,设点D(1,y),在Rt△CGD中,CD2=CG2+GD2=(2-y)2+1,在Rt△BHD中,BD2=BH2+HD2=4+y2,可以证明CD=BD,即可求y的值;
(3)过点E作EQ⊥y轴于点Q,过点F作直线FR⊥y轴于R,过点E作FP⊥FR于P,证明四边形QRPE是矩形,根据S△CEF=S矩形QRPE-S△CRF-S△EFP,代入边即可;
(4)根据平行四边形对边平行且相等的性质可以得到存在点M使得以B,C,M,N为顶点的四边形是平行四边形,点M(2,2)或M(4,-![]() )或M(-2,-
)或M(-2,-![]() ).
).
(1)将点A(-1,0),B(3,0)代入y=ax2+bx+2,
可得a=-![]() ,b=
,b=![]() ,
,
∴y=-![]() x2+
x2+![]() x+2;
x+2;
∴对称轴x=1;
(2)如图,过点D作DG⊥y轴于G,作DH⊥x轴于H,

设点D(1,y),
∵C(0,2),B(3,0),
∴在Rt△CGD中,CD2=CG2+GD2=(2-y)2+1,
∴在Rt△BHD中,BD2=BH2+HD2=4+y2,
在△BCD中,∵∠DCB=∠CBD,
∴CD=BD,
∴CD2=BD2,
∴(2-y)2+1=4+y2,
∴y=![]() ,
,
∴D(1,![]() );
);
(3)如图,过点E作EQ⊥y轴于点Q,过点F作直线FR⊥y轴于R,过点E作FP⊥FR于P,
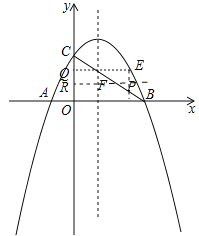
∴∠EQR=∠QRP=∠RPE=90°,
∴四边形QRPE是矩形,
∵S△CEF=S矩形QRPE-S△CRF-S△EFP-S△CQE
∵E(x,y),C(0,2),F(1,1),
∴S△CEF=EQQR-![]() ×EQQC-
×EQQC-![]() CRRF-
CRRF-![]() FPEP,
FPEP,
∴S△CEF=x(y-1)-![]() x(y-2)-
x(y-2)-![]() ×1×1-
×1×1-![]() (x-1)(y-1),
(x-1)(y-1),
∵y=-![]() x2+
x2+![]() x+2,
x+2,
∴S△CEF=-![]() x2+
x2+![]() x,
x,
∴当x=![]() 时,面积有最大值是
时,面积有最大值是![]() ,
,
此时E(![]() ,
,![]() );
);
(4)存在点M使得以B,C,M,N为顶点的四边形是平行四边形,
设N(1,n),M(x,y),
①四边形CMNB是平行四边形时,
![]() ,
,
∴x=-2,
∴M(-2,-![]() );
);
②四边形CNBM时平行四边形时,
![]() ,
,
∴x=2,
∴M(2,2);
③四边形CNNB时平行四边形时,
![]() ,
,
∴x=4,
∴M(4,-![]() );
);
综上所述:M(2,2)或M(4,-![]() )或M(-2,-
)或M(-2,-![]() ).
).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
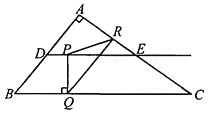
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=6,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
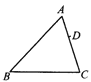
A.8B.![]() C.8或
C.8或![]() D.8或9
D.8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3)
(1)将△ABC向右平移6个单位至△A1B1C1,再将△A1B1C1绕点E(5,1)逆时针旋转90°至△A2B2C2,请按要求画出图形;
(2)在(1)的变换过程中,直接写出点C的运动路径长
(3)△A2B2C2可看成△ABC绕某点P旋转90°得到的,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人“五一”放假期间去登盘山挂月峰,甲先开车沿小路开到了距离登山入口100米的地方后,开始以10米/分钟的登山上升速度徒步登山;甲开始徒步登山同时,乙直接从登山入口开始徒步登山,起初乙以15米/分钟的登山上升速度登山,两分钟后得知甲已经在半山腰,于是乙以甲登山上升速度的3倍提速.两人相约只登到距地面高度为300米的地方,设两人徒步登山时间为![]() (分钟)
(分钟)
(Ⅰ)根据题意,填写下表:
徒步登山时间/时间 | 2 | 3 | 4 | 5 | … |
甲距地面高度/米 | 120 | ______ | 140 | ______ | … |
乙距地面高度/米 | 30 | 60 | ______ | ______ | … |
(Ⅱ)请分别求出甲、乙两人徒步登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(Ⅲ)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com