练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数图像如图，对称轴为直线，则下列叙述正确的是（　　）

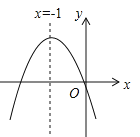
    A.ac>0B.b2<4acC.b=2aD.a+b+c>0

    【答案】C

    【解析】

    由抛物线开口方向得到a＜0，由图像与y轴的交点可知c<0，再根据抛物线的对称轴为直线x=-=-1，得到b=2a，所以b＜0，2a-b=0；根据抛物线与x轴的交点个数得到b2-4ac＞0；根据自变量为1时，对应的函数值小于0得到a+b+c＜0．

    解：∵抛物线开口向下，

    ∴a＜0，

    ∵c<0，

    ∴ac>0，故A错误；

    ∵抛物线与x轴有两个交点，

    ∴b2-4ac＞0，即b2>4ac，所以B错误；

    ∵抛物线的对称轴为直线x=-=-1，

    ∴b=2a，故C正确；

    ∵当x=1时，y＜0，

    ∴a+b+c＜0，所以D错误．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】函数y=ax2+bx+a+b（a≠0）的图象可能是（）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

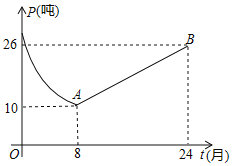
    【题目】某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数p＝（0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：

    Q＝

    （1）当8＜t≤24时，求P关于t的函数解析式；

    （2）设第t个月销售该原料药的月毛利润为W（单位：万元）．

    ①求W关于t的函数解析式；

    ②第几个月销售该原料药的月毛利润最大？对应的月销售量是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

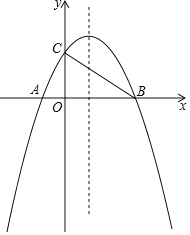
    【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx+2（a≠0）与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C，连接BC．

    （1）求该抛物线的解析式，并写出它的对称轴；

    （2）点D为抛物线对称轴上一点，连接CD、BD，若∠DCB=∠CBD，求点D的坐标；

    （3）已知F（1，1），若E（x，y）是抛物线上一个动点（其中1＜x＜2），连接CE、CF、EF，求△CEF面积的最大值及此时点E的坐标．

    （4）若点N为抛物线对称轴上一点，抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

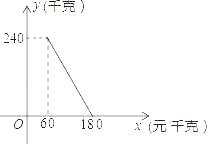
    【题目】某商店以60元/千克的单价新进一批商品，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间的函数关系式如图所示．

    （1）根据图象求出y与x的函数表达式：并写出自变量x的取值范围；

    （2）当销售单价应定为多少元时，商店获得利润达到5400元？

    （3）当销售单价应定为多少元时，商店获得利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线交轴的负半轴于点.点是轴正半轴上一点，点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点.若点的横坐标为，则的长为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线与轴、轴交与、两点，抛物线经过点、.

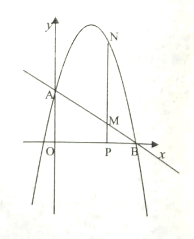
    备用图

    （1）求这个抛物线的解析式；

    （2）点为线段上一个动点，过点作垂直于轴的直线交抛物线于点，交直线于点.

    ①点是直线上方抛物线上一点，当相似时，求出点的坐标.

    ②若，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有、型两种客车，它们的载客量和租金如下表：

    型客车

    型客车

    载客量/（人/辆）

    租金/（元/辆）

    某学校计划在总费用元的限额内，租用、型客车共5辆送九年级师生集体外出活动.

    （Ⅰ）设租用型客车辆（为非负整数），根据题意，用含的式子填写下表：

    车辆数/辆

    载客量

    租金/元

    型客车

    型客车

    （Ⅱ）若九年级师生共有人，请给出能完成此项任务的最节省费用的租车方案，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：

    （元）

    19

    20

    21

    30

    （件）

    62

    60

    58

    40

    （1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．

    （2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？

    （3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？

    查看答案和解析>>

    同步练习册答案