
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴交与
轴交与![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
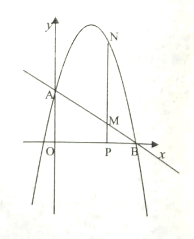

备用图
(1)求这个抛物线的解析式;
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作垂直于
作垂直于![]() 轴的直线交抛物线于点
轴的直线交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①点![]() 是直线
是直线![]() 上方抛物线上一点,当
上方抛物线上一点,当![]() 相似时,求出点
相似时,求出点![]() 的坐标.
的坐标.
②若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①
;(2)①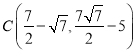 ,②
,②![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,由点A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)①设点P的坐标为(x,0),则点N的坐标为(x,-x2+![]() x+2),点C的坐标为(
x+2),点C的坐标为(![]() -x,-x2+
-x,-x2+![]() x+2),点M的坐标为(-
x+2),点M的坐标为(-![]() x+2),进而可得出MN=-x2+4x,CN=|2x-
x+2),进而可得出MN=-x2+4x,CN=|2x-![]() |,由相似三角形的性质即可得出关于x的方程,解之即可得出x的值,进而可得出点C的坐标;
|,由相似三角形的性质即可得出关于x的方程,解之即可得出x的值,进而可得出点C的坐标;
②过点N作NE⊥AB于点E,设点P的坐标为(m,0),则PM=-![]() m+2,MN=-m2+4m,利用相似三角形的性质及特殊角的三角函数值可用含m的代数式表示出BM,ME,AE的长度,再利用勾股定理即可得出关于m的一元二次方程,解之取其正值即可得出结论.
m+2,MN=-m2+4m,利用相似三角形的性质及特殊角的三角函数值可用含m的代数式表示出BM,ME,AE的长度,再利用勾股定理即可得出关于m的一元二次方程,解之取其正值即可得出结论.
解:(1)当x=0时,y=-![]() x+2=2,
x+2=2,
∴点A的坐标为(0,2);
当y=0时,-![]() x+2=0,
x+2=0,
解得:x=4,
∴点B的坐标为(4,0).
将A(0,2),B(4,0)代入y=-x2+bx+c,得:![]() ,
,
解得:![]() ,
,
∴这个抛物线的解析式为y=-x2+![]() x+2.
x+2.
(2)①当△MNC∽△BPM相似时,如图1所示.
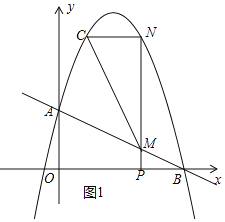
设点P的坐标为(x,0),则点N的坐标为(x,-x2+![]() x+2),点C的坐标为(
x+2),点C的坐标为(![]() -x,-x2+
-x,-x2+![]() x+2),点M的坐标为(x,-
x+2),点M的坐标为(x,-![]() x+2),
x+2),
∴MN=-x2+![]() x+2-(-
x+2-(-![]() x+2)=-x2+4x,CN=|x-(
x+2)=-x2+4x,CN=|x-(![]() -x)|=|2x-
-x)|=|2x-![]() |.
|.
∵△MNC∽△BPM,
∴![]() ,即
,即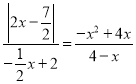 ,
,
解得:x1=![]() ,x2=-
,x2=-![]() (舍去),x3=1,x4=7(舍去),
(舍去),x3=1,x4=7(舍去),
∴![]() 或
或![]() ,
,
∴当△MNC∽△BPM时,点C的坐标为(![]() )或(
)或(![]() ).
).
②过点N作NE⊥AB于点E,如图2所示.
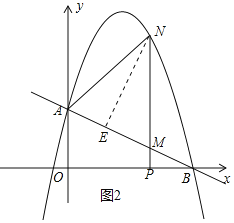
设点P的坐标为(m,0),则PM=-![]() m+2,MN=-m2+4m,
m+2,MN=-m2+4m,
∴BM=![]() PM=-
PM=-![]() m+2
m+2![]() ,ME=
,ME=![]() MN=
MN=![]() (-m2+4m),
(-m2+4m),
NE=2ME=![]() (-m2+4m),AE=tan30°×NE=
(-m2+4m),AE=tan30°×NE=![]() NE=
NE=![]() (-m2+4m),
(-m2+4m),
∴BM+ME+AE=AB,
即-![]() m+
m+![]() (-m2+4m)+
(-m2+4m)+![]() (-m2+4m)=
(-m2+4m)=![]() ,
,
整理得:(![]() )m2-(
)m2-(![]() )m=0,
)m=0,
解得:m1=0(舍去),m2=![]() ,
,
∴当∠NAB=60°时,点P的坐标为(![]() ,0),即
,0),即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,数学小组发现![]() 米高旗杆
米高旗杆![]() 的影子
的影子![]() 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高
落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高![]() 米,测得其影长为
米,测得其影长为![]() 米,同时测得
米,同时测得![]() 的长为
的长为![]() 米,
米,![]() 的长为
的长为![]() 米,测得小桥拱高(弧
米,测得小桥拱高(弧![]() 的中点到弦
的中点到弦![]() 的距离,即
的距离,即![]() 的长)为
的长)为![]() 米,则小桥所在圆的半径为( )
米,则小桥所在圆的半径为( )
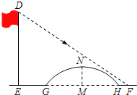
A. ![]() B. 5 C.
B. 5 C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的两个顶点
的两个顶点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,对角线
的图象上,对角线![]() 与
与![]() 的交点恰好是坐标原点
的交点恰好是坐标原点![]() ,已知点
,已知点![]() ,
,![]() .
.
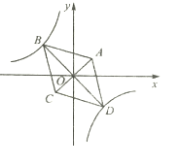
(1)求反比例函数的解析式;
(2)点![]() 是
是![]() 轴上一点,若
轴上一点,若![]() 是等腰三角形,直接写出点
是等腰三角形,直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人“五一”放假期间去登盘山挂月峰,甲先开车沿小路开到了距离登山入口100米的地方后,开始以10米/分钟的登山上升速度徒步登山;甲开始徒步登山同时,乙直接从登山入口开始徒步登山,起初乙以15米/分钟的登山上升速度登山,两分钟后得知甲已经在半山腰,于是乙以甲登山上升速度的3倍提速.两人相约只登到距地面高度为300米的地方,设两人徒步登山时间为![]() (分钟)
(分钟)
(Ⅰ)根据题意,填写下表:
徒步登山时间/时间 | 2 | 3 | 4 | 5 | … |
甲距地面高度/米 | 120 | ______ | 140 | ______ | … |
乙距地面高度/米 | 30 | 60 | ______ | ______ | … |
(Ⅱ)请分别求出甲、乙两人徒步登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(Ⅲ)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,作抛物线
中,作抛物线![]() 关于
关于![]() 轴对称的抛物线
轴对称的抛物线![]() ,再将抛物线
,再将抛物线![]() 向左平移2个单位,向上平移1个单位,得到的抛物线
向左平移2个单位,向上平移1个单位,得到的抛物线![]() 的函数解析式是
的函数解析式是![]() ,则抛物线
,则抛物线![]() 所对应的的函数解析式是( )
所对应的的函数解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
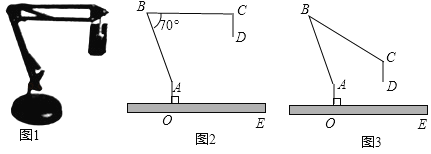
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() 于点
于点![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可转动,当
可转动,当![]() 绕点
绕点![]() 顺时针旋转时,投影探头
顺时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到0.1)
.(结果精确到0.1)
(1)如图2,![]() ,
,![]() .
.
①填空:![]() _________°;
_________°;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离.
的距离.
(2)如图3,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据:
的大小.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com