
【题目】某商店以60元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系式如图所示.
(1)根据图象求出y与x的函数表达式:并写出自变量x的取值范围;
(2)当销售单价应定为多少元时,商店获得利润达到5400元?
(3)当销售单价应定为多少元时,商店获得利润最大?最大利润是多少?
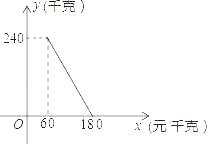
【答案】(1)y与x的函数表达式:y=﹣2x+360(60≤x≤180);(2)销售单价应定为90元或150元;(3)当销售单价定为120元时,商店获得利润最大,最大探究竟7200元.
【解析】
(1)设出一次函数的一般解析式,再代入图上已知的两点坐标,求得待定系数便可;
(2)根据“(销售单价成本)×销售数量=总利润”列出方程解答便可;
(3)根据题意求出商店获得利润w与销售单价x的函数关系式,再根据函数性质求出最值便可.
解:(1)设y与x的函数解析式为y=kx+b(k≠0),则
![]() ,
,
解得,![]() ,
,
∴y与x的函数表达式:y=﹣2x+360(60≤x≤180);
(2)由题意得,y(x﹣60)=5400,
即(x﹣60)(﹣2x+360)=5400,
解得,x1=90,x2=150,
答:销售单价应定为90元或150元;
(3)商店获得利润为w,根据题意,得
w=(x﹣60)(﹣2x+360)=﹣2(x﹣120)2+7200,
∵a=﹣2<0,则抛物线开口向下,函数有最大值,
∴当x=120时,w有最大值为7200元,
答:当销售单价定为120元时,商店获得利润最大,最大探究竟7200元.


科目:初中数学 来源: 题型:
【题目】如图所示,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:
,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:![]() ,
,![]() ,
,![]() .
.
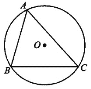
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
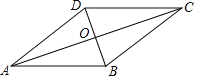
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD.
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,请你先补全图形,再求出当AB=![]() ,BD=2时,OE的长.
,BD=2时,OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
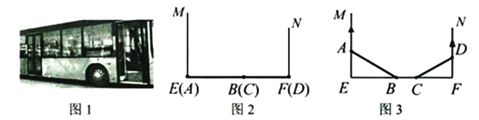
【题目】图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,![]() ,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿
,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿![]() ,
,![]() 的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知
的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知![]() .(1)如图3,当
.(1)如图3,当![]() 时,
时,![]() ______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______
______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的两个顶点
的两个顶点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,对角线
的图象上,对角线![]() 与
与![]() 的交点恰好是坐标原点
的交点恰好是坐标原点![]() ,已知点
,已知点![]() ,
,![]() .
.
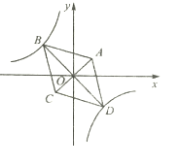
(1)求反比例函数的解析式;
(2)点![]() 是
是![]() 轴上一点,若
轴上一点,若![]() 是等腰三角形,直接写出点
是等腰三角形,直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,作抛物线
中,作抛物线![]() 关于
关于![]() 轴对称的抛物线
轴对称的抛物线![]() ,再将抛物线
,再将抛物线![]() 向左平移2个单位,向上平移1个单位,得到的抛物线
向左平移2个单位,向上平移1个单位,得到的抛物线![]() 的函数解析式是
的函数解析式是![]() ,则抛物线
,则抛物线![]() 所对应的的函数解析式是( )
所对应的的函数解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在关于“折纸问题”的数学活动课中,小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH,再将纸片EFGH按如图所示分别沿MN、P2折叠,使点E,G落在线段PN上点E,G处,当PNEF时,若阴影部分的周长之和为16,△AEH,△CFG的面积之和为12,则菱形纸片ABCD的一条对角线BD的长为_____.
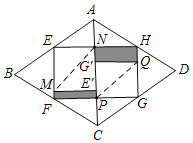
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com