
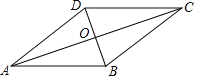
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD.
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,请你先补全图形,再求出当AB=![]() ,BD=2时,OE的长.
,BD=2时,OE的长.
【答案】(1)见解析;(2)2.
【解析】
(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;
(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA,即可得出结论.
(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC平分∠BAD.
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形;
(2)解:补全图形如图所示:
∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=![]() BD=1,
BD=1,
在Rt△AOB中,AB=![]() ,OB=1,
,OB=1,
∴OA=![]() =2,
=2,
∴OE=OA=2.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
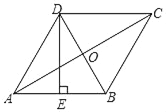
【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A. 18 B. 18![]() C. 9
C. 9![]() D. 6
D. 6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
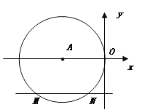
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2) C.(-1.5,-2) D.(1.5,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
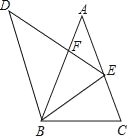
【题目】如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
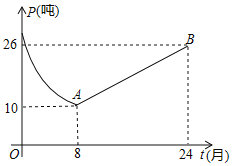
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数p=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:
Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为W(单位:万元).
①求W关于t的函数解析式;
②第几个月销售该原料药的月毛利润最大?对应的月销售量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
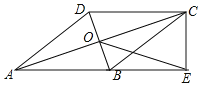
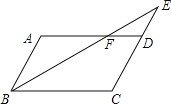
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为a,则平行四边形ABCD的面积为 ▲ (用a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
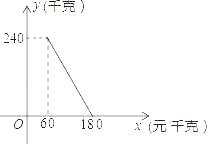
【题目】某商店以60元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系式如图所示.
(1)根据图象求出y与x的函数表达式:并写出自变量x的取值范围;
(2)当销售单价应定为多少元时,商店获得利润达到5400元?
(3)当销售单价应定为多少元时,商店获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com