
【题目】如图所示,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:
,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:![]() ,
,![]() ,
,![]() .
.
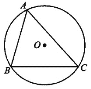
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
【答案】(1)60°;(2)![]()
【解析】
(1)连接BO并延长交⊙O于点D,连接CD,得到∠DCB=90°,BD=4,再解直角三角形即可解答.
(2)因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积最大,此时点A应落在优弧BC的中点处,过OE⊥BC于点E,延长EO交 O于点A,则A为优弧BC的中点,连接AB,AC,则AB=AC,由圆周角定理可求出∠BAE的度数,在Rt△ABE中,利用锐角三角函数的定义及特殊角的三角函数值可求出AE的长,由三角形的面积公式即可解答.
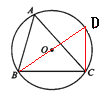
(1)连接BO并延长交⊙O于点D,连接CD.
∵ BD是直径,∴ BD=4,∠DCB=90°.
在Rt△DBC中,![]() ,
,
∴ ∠BDC=60°,∴ ∠BAC=∠BDC=60°.
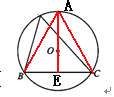
(2)因为△ABC的边BC的长不变,所以当BC边上的高最大时,△ABC的面积最大,此时点A应落在优弧BC的中点处.
过O作OE⊥BC于点E,延长EO交⊙O于点A,则A为优孤BC的中点.连结AB,AC,
则AB=AC,∠BAE![]() ∠BAC=30°.
∠BAC=30°.
在Rt△ABE中,
∵ BE![]() ,∠BAE=30°,
,∠BAE=30°,
∴ ![]() ,
,
∴ ![]() .
.
答:△ABC面积的最大值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
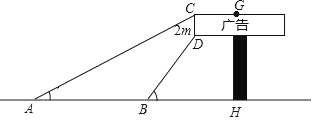
【题目】数学社团小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() =1.73,要求结果精确得到0.1m)
=1.73,要求结果精确得到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
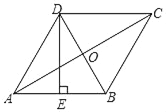
【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A. 18 B. 18![]() C. 9
C. 9![]() D. 6
D. 6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
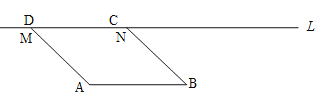
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=6![]() ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为
,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为![]() ,并且CD⊥AC,则BC的长为________.
,并且CD⊥AC,则BC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )
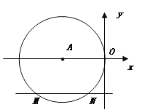
A.(-1,-2) B.(1,2) C.(-1.5,-2) D.(1.5,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
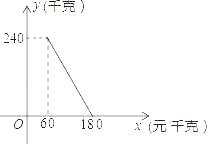
【题目】某商店以60元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系式如图所示.
(1)根据图象求出y与x的函数表达式:并写出自变量x的取值范围;
(2)当销售单价应定为多少元时,商店获得利润达到5400元?
(3)当销售单价应定为多少元时,商店获得利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com