
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
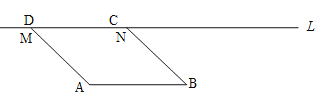
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
【答案】(1)![]() ;(2)t=
;(2)t=![]() -1或
-1或![]() +1.
+1.
【解析】
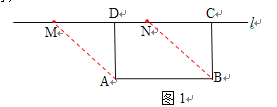
(1)根据矩形和等腰三角形的性质得到MD=AD,故可求解;
(2)根据题意可分两种情况作图,再根据菱形的性质与勾股定理进行求解.
解(1)如图1,根据矩形的性质可知∠DAB=∠ADC=90°,故∠ADM=45°,又AD=![]() ,∴MD=
,∴MD=![]() ,
,
故当t=![]() 时,□ABCD为矩形;
时,□ABCD为矩形;
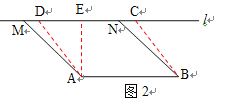
(2)①如图2,过A作AE⊥MN
当四边形ABCD为菱形时,
∴AD=AB=2
在Rt△ADE中
DE=![]() =1
=1
在Rt△AME中
∠MAE=1350-900=450
∴ME=AE=![]()
MD=![]() -1
-1
t=![]() -1
-1
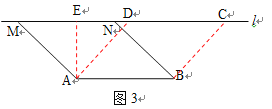
②如图3,过A作AE⊥MN
当四边形ABCD为菱形时,
∴AD=AB=2
由①易得
DE=1, ME=![]()
MD=![]() +1
+1
t=![]() +1
+1
∴线段运动![]() -1或
-1或![]() +1秒时,四边形ABCD为菱形
+1秒时,四边形ABCD为菱形


科目:初中数学 来源: 题型:
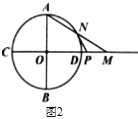
【题目】已知,![]() 的半径为1;直线
的半径为1;直线![]() 经过圆心
经过圆心![]() ,交
,交![]() 于
于![]() 、
、![]() 两点,直径
两点,直径![]() ,点
,点![]() 是直线
是直线![]() 上异于
上异于![]() 的一个动点,直线
的一个动点,直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是直线
是直线![]() 上另一点,且
上另一点,且![]() .
.
(Ⅰ)如图1,点![]() 在
在![]() 的内部,求证:
的内部,求证:![]() 是
是![]() 的切线;
的切线;
(Ⅱ)如图2,点![]() 在
在![]() 的外部,且
的外部,且![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
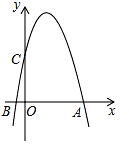
【题目】如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
(3)抛物线上是否存在点P,使△ACP为直角三角形?若存在,有几个?写出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:
,点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据:![]() ,
,![]() ,
,![]() .
.
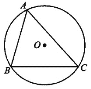
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
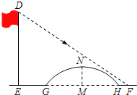
【题目】如图所示,数学小组发现![]() 米高旗杆
米高旗杆![]() 的影子
的影子![]() 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高
落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高![]() 米,测得其影长为
米,测得其影长为![]() 米,同时测得
米,同时测得![]() 的长为
的长为![]() 米,
米,![]() 的长为
的长为![]() 米,测得小桥拱高(弧
米,测得小桥拱高(弧![]() 的中点到弦
的中点到弦![]() 的距离,即
的距离,即![]() 的长)为
的长)为![]() 米,则小桥所在圆的半径为( )
米,则小桥所在圆的半径为( )
A. ![]() B. 5 C.
B. 5 C. ![]() D. 6
D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com