
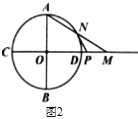
【题目】已知,![]() 的半径为1;直线
的半径为1;直线![]() 经过圆心
经过圆心![]() ,交
,交![]() 于
于![]() 、
、![]() 两点,直径
两点,直径![]() ,点
,点![]() 是直线
是直线![]() 上异于
上异于![]() 的一个动点,直线
的一个动点,直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是直线
是直线![]() 上另一点,且
上另一点,且![]() .
.
(Ⅰ)如图1,点![]() 在
在![]() 的内部,求证:
的内部,求证:![]() 是
是![]() 的切线;
的切线;
(Ⅱ)如图2,点![]() 在
在![]() 的外部,且
的外部,且![]() ,求
,求![]() 的长.
的长.

科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
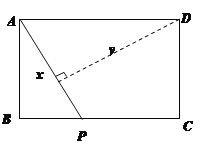
A.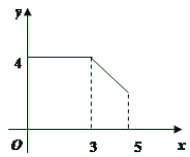 B.
B.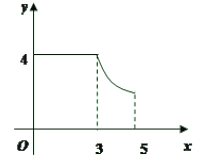
C.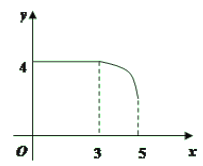 D.
D.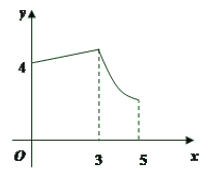
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心____点,按顺时针方向旋转___度得到;
(3)若BC=8,DE=2,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中AB=8![]() ,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=![]() ;
;

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )

A. 50m B. 100m C. 160m D. 200m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学社团小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() =1.73,要求结果精确得到0.1m)
=1.73,要求结果精确得到0.1m)
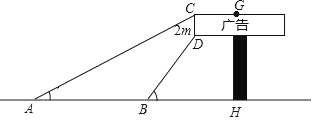
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
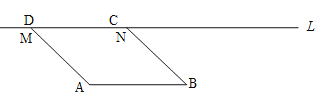
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com