
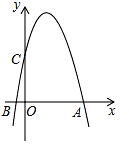
【题目】如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
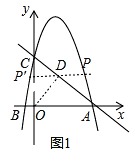
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
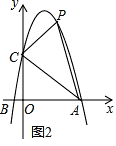
(3)抛物线上是否存在点P,使△ACP为直角三角形?若存在,有几个?写出所有符合条件的点P的坐标;若不存在,说明理由.
【答案】(1)y=﹣x2+5x+6;(2)点M(![]() );(3)点P的坐标为(﹣2,﹣8)或(4,10)或(2+2
);(3)点P的坐标为(﹣2,﹣8)或(4,10)或(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() ).
).
【解析】
(1)已知C(0,6),由交点式设抛物线解析式为y=a(x+1)(x﹣6),把C点代入即可求解;
(2)先求出抛物线的对称轴,再作出点B关于抛物线对称轴的对称点(即为A点),连接AC交对称轴于点M,再求AC与对称轴的交点可得结果;
(3)由点P在抛物线上,可先设出P点坐标,然后分别表示出PC2、PA2 、AC2,再按照∠PAC=90°、∠PCA=90°、∠APC=90°三种情况分别求解即可.
(1)当x=0时,y=ax2+bx+6=6,则C(0,6),
设抛物线的解析式为y=a(x+1)(x﹣6),
把C(0,6)代入得a1(﹣6)=6,解得a=﹣1,
∴抛物线的解析式为y=﹣(x+1)(x﹣6),即y=﹣x2+5x+6;
(2)∵抛物线的对称轴是直线x=![]() ,直线AC的解析式为y=-x+6,点B关于对称轴直线x=
,直线AC的解析式为y=-x+6,点B关于对称轴直线x=![]() 的对称点为点A,
的对称点为点A,
∴连接AC,交直线x=![]() 于点M,此时点M满足CM+BM最小,
于点M,此时点M满足CM+BM最小,
当x=![]() 时,y=
时,y=![]() ,∴点M(
,∴点M(![]() )
)
(3)设P点坐标为(x,﹣x2+5x+6),存在4个点P,使△ACP为直角三角形.
PC2=x2+(﹣x2+5x)2,PA2=(x﹣6)2+(﹣x2+5x+6)2,AC2=62+62=72,
当∠PAC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+72=x2+(﹣x2+5x)2,
整理得x2﹣4x﹣12=0,得x1=6(舍去),x2=﹣2,此时P点坐标为(﹣2,﹣8);
当∠PCA=90°,∵PC2+AC2=PA2,
72+x2+(﹣x2+5x)2=(x﹣6)2+(﹣x2+5x+6)2,
整理得x2﹣4x=0,解得x1=0(舍去),x2=4,此时P点坐标为(4,10);
当∠APC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+x2+(﹣x2+5x)2=72,
整理得x3﹣10x2+20x+24=0,
x3﹣10x2+24x﹣4x+24=0,
x(x2﹣10x+24)﹣4(x﹣6)=0,
x(x﹣4)(x﹣6)﹣4(x﹣6)=0,
(x﹣6)(x2﹣4x﹣4)=0,
而x﹣6≠0,
所以x2﹣4x﹣4=0,解得x1=2+2![]() ,x2=2﹣2
,x2=2﹣2![]() ,此时P点坐标为(2+2
,此时P点坐标为(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() );
);
综上所述,符合条件的点P的坐标为(﹣2,﹣8)或(4,10)或(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心____点,按顺时针方向旋转___度得到;
(3)若BC=8,DE=2,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
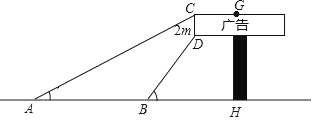
【题目】数学社团小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() =1.73,要求结果精确得到0.1m)
=1.73,要求结果精确得到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,3),与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2+4ac>0;②c﹣a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )

A.②③ B.①③ C.①②③ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图所示.其中阅读时间是8~10小时的频数和频率分别是( )
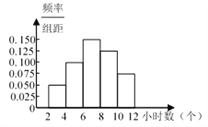
A. 15和0.125 B. 15和0.25 C. 30和0.125 D. 30和0.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
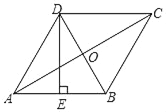
A. 18 B. 18![]() C. 9
C. 9![]() D. 6
D. 6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=2cm,线段AB与直线l之间的距离为![]() cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
cm,线段CD的起始位置在MN处,此时∠MAB=1350,现将线段CD在直线l上向右移动,移动速度为1cm/s,运动时间为ts.
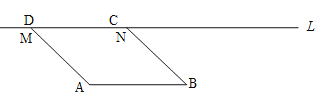
(1)当t=____s时,□ABCD为矩形;
(2)线段CD在直线l上移动过程中,当□ABCD为菱形时,求线段CD运动时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com