
【题目】现有![]() 、
、![]() 型两种客车,它们的载客量和租金如下表:
型两种客车,它们的载客量和租金如下表:
|
| |
载客量/(人/辆) |
|
|
租金/(元/辆) |
|
|
某学校计划在总费用![]() 元的限额内,租用
元的限额内,租用![]() 、
、![]() 型客车共5辆送九年级师生集体外出活动.
型客车共5辆送九年级师生集体外出活动.
(Ⅰ)设租用![]() 型客车
型客车![]() 辆(
辆(![]() 为非负整数),根据题意,用含
为非负整数),根据题意,用含![]() 的式子填写下表:
的式子填写下表:
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
(Ⅱ)若九年级师生共有![]() 人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)能完成此项任务的最节省费用的租车方案 是
;(Ⅱ)能完成此项任务的最节省费用的租车方案 是![]() 型客车3辆,
型客车3辆,![]() 型客车2辆
型客车2辆
【解析】
(Ⅰ)B型客车载客量=车辆数×每辆车载客量;B型客车租金=车辆数×每辆车租金
(Ⅱ)当租用A型客车x辆(x为非负整数)时,设租车总费用为y元,则两种客车的总费用为y=400x+280(5-x)=120x+1400,为使195名九年级师生有车坐,x不能小于3;为使租车费用不超过1900元,x不能超过4,即可求解
(Ⅰ)150-30x,1400-280x.
(Ⅱ)能完成此项任务的最节省费用的租车方案 是A型客车3辆,B型客车2辆.
理由:当租用A型客车x辆(x为非负整数)时,设租车总费用为y元,
则 两种客车的总费用为y=400x+280(5-x)=120x+1400;
为使195名九年级师生有车坐,x不能小于3;为使租车费用不超过1900元,x不能超过4.综合起来可知x的取值为3或4.
∵120>0,∴在函数y=4120x+1400中,y随x的增大而增大.
∴当x=3时,y取得最小值.
即能完成此项任务的最节省费用的租车方案 是A型客车3辆,B型客车2辆.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
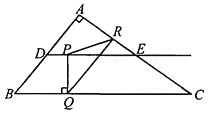
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人“五一”放假期间去登盘山挂月峰,甲先开车沿小路开到了距离登山入口100米的地方后,开始以10米/分钟的登山上升速度徒步登山;甲开始徒步登山同时,乙直接从登山入口开始徒步登山,起初乙以15米/分钟的登山上升速度登山,两分钟后得知甲已经在半山腰,于是乙以甲登山上升速度的3倍提速.两人相约只登到距地面高度为300米的地方,设两人徒步登山时间为![]() (分钟)
(分钟)
(Ⅰ)根据题意,填写下表:
徒步登山时间/时间 | 2 | 3 | 4 | 5 | … |
甲距地面高度/米 | 120 | ______ | 140 | ______ | … |
乙距地面高度/米 | 30 | 60 | ______ | ______ | … |
(Ⅱ)请分别求出甲、乙两人徒步登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(Ⅲ)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,作抛物线
中,作抛物线![]() 关于
关于![]() 轴对称的抛物线
轴对称的抛物线![]() ,再将抛物线
,再将抛物线![]() 向左平移2个单位,向上平移1个单位,得到的抛物线
向左平移2个单位,向上平移1个单位,得到的抛物线![]() 的函数解析式是
的函数解析式是![]() ,则抛物线
,则抛物线![]() 所对应的的函数解析式是( )
所对应的的函数解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
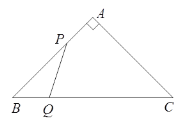
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
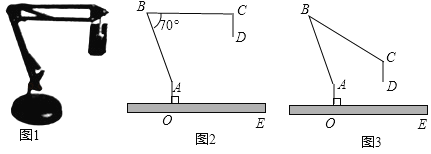
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() 于点
于点![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可转动,当
可转动,当![]() 绕点
绕点![]() 顺时针旋转时,投影探头
顺时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到0.1)
.(结果精确到0.1)
(1)如图2,![]() ,
,![]() .
.
①填空:![]() _________°;
_________°;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离.
的距离.
(2)如图3,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据:
的大小.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com