
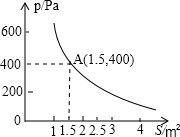
 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.分析 (1)由图可知1.5×400=600为定值,即k=600,易求出解析式.
(2)将S=0.4代入(1)中所求解析式,计算即可求出函数值p.
(3)压强不超过6000Pa,即p≤6000时,求相对应的自变量的范围.
解答 解:(1)设p=$\frac{k}{S}$.
把A(1.5,400)代入,得400=$\frac{k}{1.5}$,
k=1.5×400=600,
则p=$\frac{600}{S}$(S>0).
(2)当S=0.4时,p=$\frac{600}{0.4}$=1500,即压强是1500Pa.
(3)由题意知$\frac{600}{S}$≤6000,
解得S≥0.1,
即木板面积至少要有0.1m2.
点评 此题主要考查反比例函数在实际生活中的应用,解题的关键是从实际问题中整理出函数模型,用反比例函数的知识解决实际问题,同学们要认真观察图象得出正确的结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com