
 如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$. 分析 作ED⊥BF于D,由已知条件和等腰直角三角形的性质得出∠CAE=∠FBC,证出∠1=∠2,得出△ACE∽△BFC,由相似三角形的对应边成比例得出AC•BC=AE•BF=AC2,求出AC2=2$\sqrt{5}$,得出DE2=4$\sqrt{5}$,由勾股定理求出EF即可.
解答 解:作ED⊥BF于D,如图所示: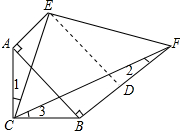
∵∠ECF=45°,∠ACB=90°,
∴∠1+∠3=45°,
∵AC=BC,
∴∠ABC=∠CAB=45°,
∵AE⊥AB,BF⊥AB,
∴∠EAB=∠ABF=90°,
∴∠CAE=45°+90°=135°=∠FBC,
∴∠2+∠3=45°,
∴∠1=∠2,
∴△ACE∽△BFC,
∴$\frac{AC}{BF}=\frac{AE}{BC}$,
∴AC•BC=AE•BF=AC2,
∴AC2=$\sqrt{2}$×$\sqrt{10}$=2$\sqrt{5}$,
∴DE2=AB2=2AC2=4$\sqrt{5}$,
∴EF=$\sqrt{D{E}^{2}+D{F}^{{\;}^{2}}}$=$\sqrt{4\sqrt{5}+(\sqrt{10}-\sqrt{2})^{2}}$=2$\sqrt{3}$;
故答案为:2$\sqrt{3}$.
点评 本题考查了等腰直角三角形的性质、相似三角形的判定与性质、勾股定理;由三角形相似得出AC2的值是解决问题的关键.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:选择题
| A. | (6.-3) | B. | (-3,6) | C. | (6,3) | D. | (3,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.
如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
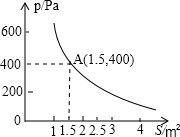 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{3x-y=1}\\{6x+2y=70}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-3x=1}\\{6x+2y=70}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-3x=1}\\{2x+6y=70}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=1}\\{2x+6y=70}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com